В некоторых случаях эмиссионная граница находится в области, где концентрация нейтралов мала, тогда ими можно пренебречь или учесть в виде малых добавок. В этом случае пространственное положение эмиссионной границы устанавливается под влиянием двух факторов: эмиссионной способности плазмы, проникающей в вакуум, и величины напряжения, ускоряющего частицы. Для получения основных результатов в аналитическом виде будем рассматривать плоский плазменный диод.
Параметры промежутка: расстояние между плоскостью анода и экстрактора xэ; напряжение экстрактора U э и концентрация проникающей плазмы должны быть выбраны таким образом, чтобы в рабочем режиме граница плазмы xгр находилась в ускоряющем промежутке. В расчетах будем пренебрегать изменением потенциала в проникающей плазме в зависимости от x, так как оно значительно меньше U э (обычно U э≥1 кВ).
На границе плазмы должны быть выполнены два условия:
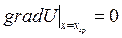 и и 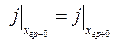
|
где 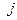 - плотность тока слева и справа от границы плазмы (в плазме и вакууме).
- плотность тока слева и справа от границы плазмы (в плазме и вакууме).
Плотность тока заряженных частиц в плазме определяется выражением
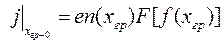 , ,
|
где e – заряд электрона, 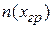 - концентрация частиц в плоскости границы плазмы,
- концентрация частиц в плоскости границы плазмы, 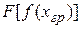 - функция, зависящая от рода извлекаемых частиц, и их функции распределения по скоростям. В случае извлечения электронов
- функция, зависящая от рода извлекаемых частиц, и их функции распределения по скоростям. В случае извлечения электронов
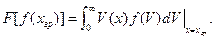
|
При извлечении ионов из плазмы с максвелловским распределением электронов по скоростям:
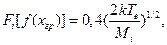
|
где 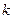 – постоянная Больцмана,
– постоянная Больцмана, 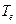 - температура электронов в плазме,
- температура электронов в плазме, 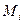 - масса иона.
- масса иона.
В вакуумном промежутке должен выполняться закон «степени 3/2», который запишем в виде
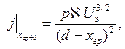
|
где 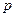 - параметр, зависящий от рода извлекаемых частиц (для электронов он равен 2,33 10-6, для ионов - 5,48 10-8 µ-1/2, µ - атомный номер иона);
- параметр, зависящий от рода извлекаемых частиц (для электронов он равен 2,33 10-6, для ионов - 5,48 10-8 µ-1/2, µ - атомный номер иона); 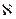 - параметр, учитывающий искажение потенциала в ускоряющей промежутке за счет частичной компенсации объемного заряда ускоряемых частиц, частицами другого знака.
- параметр, учитывающий искажение потенциала в ускоряющей промежутке за счет частичной компенсации объемного заряда ускоряемых частиц, частицами другого знака.
Распределение концентрации проникающей в вакуум плазмы, может быть описано выражением вида
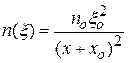 , ,
|
где 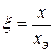 - безразмерная координата;
- безразмерная координата; 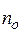 – концентрация заряженных частиц в плоскости анода;
– концентрация заряженных частиц в плоскости анода; 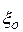 - безразмерная постоянная, которая необходима для того, чтобы
- безразмерная постоянная, которая необходима для того, чтобы 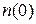 была конечной величиной.
была конечной величиной.
Координата границы проникающей плазмы, которая устанавливается в зависимости от параметров промежутка, определяется выражением
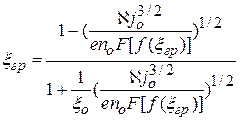 . .
|
Вольтамперную характеристику промежутка с подвижной плазменной границей можно получить в виде:
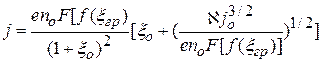 . .
|
Если 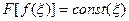 , то
, то 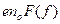 будет выражать плотность тока насыщения
будет выражать плотность тока насыщения 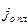 частиц из плазмы, когда ее граница расположена в плоскости газоразрядного анода источника. Выражение для вольтамперной характеристики в этом случае имеет вид:
частиц из плазмы, когда ее граница расположена в плоскости газоразрядного анода источника. Выражение для вольтамперной характеристики в этом случае имеет вид:
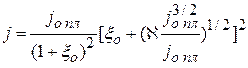 . .
|
Полученное выражение для вольтамперной характеристики отражает влияние параметров проникающей плазмы через 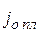 и
и 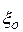 , а также величины ускоряющего напряжения, геометрии промежутка и условий компенсации пространственного заряда ускоряемых частиц через
, а также величины ускоряющего напряжения, геометрии промежутка и условий компенсации пространственного заряда ускоряемых частиц через 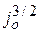 и
и 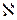 .
.
Проанализируем полученное решение. В случае, когда 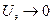 , что равносильно
, что равносильно 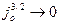 , имеем
, имеем
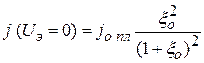 . .
|
то есть ток частиц остается конечной величиной, определяемой параметрами проникающей плазмы в плоскости экстрактора, в то время как в обычном диоде в приближении закона «степени 3/2» 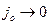 . При возрастании напряжения граница плазмы перемещается к аноду (
. При возрастании напряжения граница плазмы перемещается к аноду (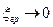 ) и при
) и при 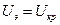 ,
, 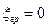 . Величина
. Величина 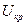 может быть определена из выражения
может быть определена из выражения
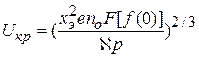 . .
|
При критическом напряжении на экстракторе ток через промежуток будет равен 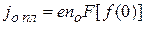 .
.
 2015-07-03
2015-07-03 361
361








