Визначник квадратної матриці 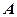 позначають
позначають 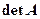 (скорочення від латинської назви детермінант), або |
(скорочення від латинської назви детермінант), або | 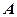 |. Наприклад, якщо
|. Наприклад, якщо
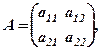 то
то 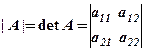 .
.
Теорема. Визначник добутку двох квадратних матриць 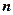 -го порядку дорівнює добуткові їх визначників, тобто
-го порядку дорівнює добуткові їх визначників, тобто
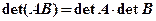 , або
, або 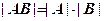 . (1)
. (1)
Рівність перевіримо для матриць другого порядку.
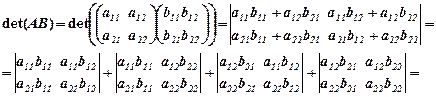
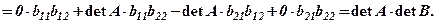
Приклад. Перевірити рівність (1) для таких матриць

Розв’язання. Обчислимо спочатку визначники заданих матриць та добуток їх
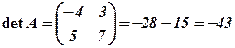 ;
; 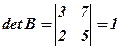 ,
,
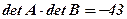 .
.
Знайдемо тепер добуток матриць 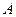 і
і 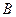 і теж обчислимо їх визначник
і теж обчислимо їх визначник
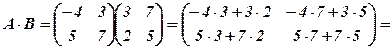
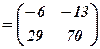 .
. 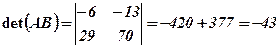 .
.
Отже, 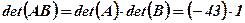 .
.
Приклади. Знайти визначники матриць:
1. 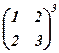 . 2
. 2 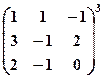 . 3.
. 3. 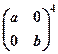 .
.
4. 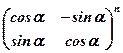 . 5.
. 5. 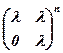 . 6.
. 6. 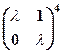 .
.
Для поданих матриць 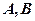 знайти їх добуток
знайти їх добуток 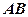 та обчислити визначники. Результат перевірити за допомогою теореми.
та обчислити визначники. Результат перевірити за допомогою теореми.
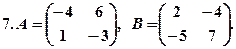
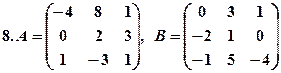
Відповіді. 1. -1. 2. 343. 3. 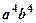 . 4. 1. 5.
. 4. 1. 5. 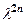 . 6.
. 6. 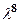 .
.
7. 6,-6,-36. 8. -6, -33, 198.
 2015-07-03
2015-07-03 569
569








