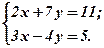
Розв’язання. Запишемо матриці
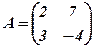 ,
, 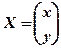 ,
, 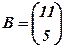 .
.
У матричному вигляді система запишеться
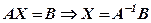 .
.
Визначник матриці 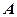
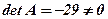 , існує обернена матриця
, існує обернена матриця 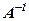 . Її алгебраїчні допованення
. Її алгебраїчні допованення
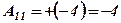 ;
; 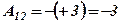 ;
;
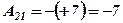 ;
; 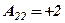 .
.
Обернена матриця
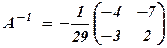 .
.
Розв’язком системи є матриця
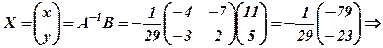
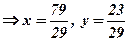 .
.
Перевірка: 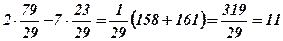 ,
,
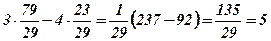 .
.
Зауваження.
1. Розглянутий матричний спосіб на прикладі лінійних систем третього порядку узагальнюється на системи вищих порядків.
2. В більш загальних випадках в матричних рівняннях
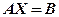
матриці 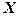 і
і 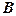 можуть мати інші розміри і бути не тільки матрицями стовпцями.
можуть мати інші розміри і бути не тільки матрицями стовпцями.
3. При розв’язанні матричних рівнянь вигляду
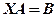
домножують на обернену матрицю 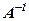 справа, тобто
справа, тобто
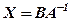 .
.
 2015-07-03
2015-07-03 341
341








