Алгоритм метода градиентного спуска

1. Задать начальную точку х, погрешность ε, начальный шаг β и вычислить y=f(x).

2. Вычислить ∇f(x), проверить условие ||∇f(x||< ε. Если оно выполнено, то расчёт закончен, ответ - пара значений {x, y}, иначе перейти к шагу 3.

3. Вычислить x₁= x - β ∙∇f(x) и y₁=f(x₁).

4. Если y₁ < y, то положить x=x₁, y=y₁ и перейти к шагу 2, иначе к шагу 5.

5. Положить β = β / 2 и перейти к шагу 3.

Пример.

Выполнить два шага решения задачи поиска минимума функции

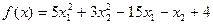
методом наискорейшего спуска, начиная расчёт из точки x₀= (7,4) с начальным шагом β = 0.1 и величиной ε=0.01.

Решение.

Вычисляем f(x) = f(7;4) = 188.

Находим градиент заданной функции:

∇f(x) =(10x₁ -15; 6x₂ -1). Тогда p = (-10x₁+15; -6x₂ +1).

Проверим выполнение условия ||∇f(x||< ε. Имеем

||∇f(7;4)|| = ||(70 -15; 24 -1) || = ||(55; 23) || ⋲ 59.6 > ε

Вычислим x₁= x - β ∙∇f(x) = (7;4) – 0.1 ∙ (55;23) = (7- 5,5; 4 – 2,3) = (1,5; 1,7)

и y₁ = f(x₁) = -0,28.

Т.к. y₁ < y, то x = x₁ = (1,5; 1,7), y = y₁ = - 0,28.

Вычисляем ∇f(x) = (0; 9,2), проверяем условие ||∇f(x||< ε: ||∇f(x|| = 9,2 > ε.

Вычисляем x₁= x - β ∙∇f(x) = (1,5; 1,7) – 0,1 ∙ (0; 9,2) = (1,5; 0,78) и y₁ = f(x₁) = - 6,2048.

Т.к. y₁ = - 6,2048 < y - 0,28, то x = x₁ = (1,5; 0,78) y = y₁ = - 6,2048.

Вычисляем ∇f(x) = (0; 3,68), проверяем условие ||∇f(x||< ε: ||∇f(x|| = 3,68 > ε.

Вычисляем x₁= x - β ∙∇f(x) = (1,5; 0,78) – 0,1 ∙ (0; 3,68) = (1,5; 0,412) и y₁ = f(x₁) = - 7,1528.

И т.д.