Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения.
При табличном способе задания закона распределения первая строка таблицы содержит возможные значения случайной величины (обычно в порядке возрастания), а вторая – соответствующие вероятности (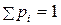 ):
):
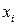 | 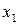 | 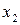 | … | 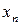 |
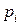 | 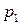 | 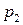 | … | 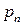 |
Дискретная случайная величина имеет биномиальный закон распределения (закон распределения Бернулли), если она принимает целочисленные неотрицательные значения 0, 1, 2, 3, …, m, …, n с вероятностями, вычисляемыми по формуле Бернулли:
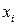 | … | m | … | n | ||
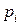 | 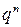 | 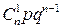 | … | 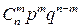 | … | 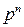 |
где 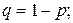
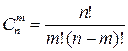 - число сочетаний из n элементов по m.
- число сочетаний из n элементов по m.
Пример 2. На некотором участке дороги 60% водителей соблюдают предусмотренный правилами скоростной режим. Составить закон распределения числа водителей, соблюдающих установленные ограничения по скорости, из пяти проехавших.
Случайная величина Х – число водителей, соблюдающих установленные ограничения по скорости из пяти проехавших. В 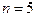 независимых испытаниях вероятность того, что скоростной режим не нарушен, по условию постоянна и равна:
независимых испытаниях вероятность того, что скоростной режим не нарушен, по условию постоянна и равна: 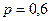 . Следовательно, вероятность нарушения:
. Следовательно, вероятность нарушения: 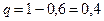 . Тогда биномиальный закон распределения числа водителей имеет вид:
. Тогда биномиальный закон распределения числа водителей имеет вид:
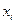 | ||||||
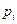 | 0,01024 | 0,0768 | 0,2304 | 0,3456 | 0,2592 | 0,07776 |
Дискретная случайная величина имеет закон распределения Пуассона с параметром 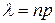 , если она принимает целочисленные неотрицательные значения 0, 1, 2, 3, …, m, … с вероятностями, вычисляемыми по формуле Пуассона. Т. к. вероятность наступления события в каждом испытании мала (при
, если она принимает целочисленные неотрицательные значения 0, 1, 2, 3, …, m, … с вероятностями, вычисляемыми по формуле Пуассона. Т. к. вероятность наступления события в каждом испытании мала (при 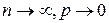 ), закон распределения Пуассона еще называют законом редких событий.
), закон распределения Пуассона еще называют законом редких событий.
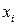 | … | m | … | ||
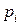 | 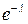 | 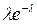 | … | 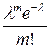 | … |
Пример 3. Вероятность попадания в цель при одном выстреле равна 0,015. Сделано 600 выстрелов. Какова вероятность того, что число попаданий в цель не меньше 7 и не большее 10?
В данном случае 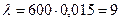 . Предполагая закон распределения Пуассона, имеем:
. Предполагая закон распределения Пуассона, имеем:
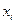 | ||||
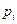 | 0,1171 | 0,1318 | 0,1318 | 0,1186 |
Следовательно, 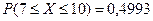 .
.
 2015-07-03
2015-07-03 2471
2471