Между изменением значений варьирующего признака и их частотами существует определенная зависимость. Как правило, частоты в вариационных рядах с ростом значения варьирующего признака первоначально увеличиваются, а затем после достижения какой-то максимальной величины в середине ряда уменьшаются (см. табл. 5.3). Значит, частоты в этих рядах изменяются закономерно в связи с изменением варьирующего признака.
Анализ вариационных рядов предполагает выявление закономерностей распределения, определение и построение (получение) некой теоретической (вероятностной) формы распределения.
Графическое изображение вариационного ряда принимает вид плавной кривой, именуемой кривой распределения.
Примером фактической кривой распределения является полигон распределения, поскольку в нем отражаются как общие, так и случайные условия, определяющие распределение.
Теоретической кривой распределения называется такая, которая выражает общую закономерность данного типа распределения в чистом виде, исключающего влияние случайных для данного типа закономерностей факторов. Теоретическая кривая распределения, выражая функциональную связь между изменением варьирующего признака и изменением частот, характеризует определенный тип распределения. В практике статистического исследования встречаются различные распределения: нормальное, биномиальное, Пуассона и др. Большое познавательное значение имеет сопоставление фактических кривых распределения с теоретическими. В статистике наиболее часто для этого пользуются нормальным распределением.
Распределение непрерывной случайной величины х называют нормальным N (x, σ), если соответствующая ей плотность распределения выражается формулой
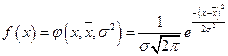 или
или 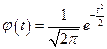 ,
,
где х – значение изучаемого признака;
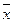 - средняя арифметическая ряда;
- средняя арифметическая ряда;
σ2 – дисперсия значений изучаемого признака;
σ – среднее квадратическое отклонение изучаемого признака;
π = 3,1415 – постоянное число (отношение длины окружности к ее диаметру);
е = 2,7182 – основание натурального логарифма;
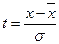 - нормированное отклонение.
- нормированное отклонение.
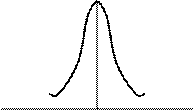
При графическом изображении плотности распределения f(x) получается кривая нормального распределения, симметричная относительно вертикальной прямой 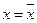 (рис. 5.6), поэтому величину
(рис. 5.6), поэтому величину 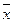 называют центром распределения. Кривая имеет максимум в точке соответствующей значению
называют центром распределения. Кривая имеет максимум в точке соответствующей значению 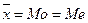 .
.
 |


-σ 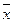 σ
σ
Рис. 5.6. Кривая нормального распределения
Кривая нормального распределения имеет две точки перегиба на расстоянии ± σ от 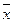 .
.
В пределах 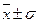 при нормальном распределении заключается 68,3 % всех членов распределения (исследуемых единиц). Нормальное распределение далее характеризуется тем, что 95,4 % всех членов распределения находятся в пределах, ограниченных точками
при нормальном распределении заключается 68,3 % всех членов распределения (исследуемых единиц). Нормальное распределение далее характеризуется тем, что 95,4 % всех членов распределения находятся в пределах, ограниченных точками 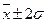 , а 99,7 % всех членов – в пределах, ограниченных точками
, а 99,7 % всех членов – в пределах, ограниченных точками 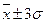 .
.
Нормальное распределение в статистике часто служит моделью для выяснения степени и характера отклонения от нее фактического распределения.
Для изучения характера вариации используются средние значения разных степеней отклонений отдельных величин признака от его средней арифметической величины. Эти показатели получили название центральных моментов распределения порядка, соответствующего степени, в которую возводятся отклонения (табл. 5.9). Величина третьего момента μ3 зависит, как и его знак, от преобладания положительных кубов отклонений над отрицательными кубами и наоборот. При нормальном и любом другом строго симметричном распределении сумма положительных кубов строго равна сумме отрицательных кубов.
Таблица 5.9
| Порядок момента | Формула расчета | |
| По несгруппированным данным | По сгруппированным данным | |
| Первый (μ1) | 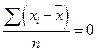 | 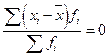 |
| Второй (μ2) | 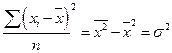 | 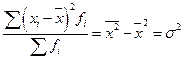 |
| Третий (μ3) | 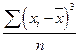 | 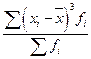 |
| Четвертый (μ4) | 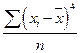 | 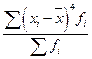 |
Центральный момент третьего порядка используется при исчислении степени асимметрии распределения.
При симметричном распределении варианты, равноудаленные от 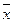 , имеют одинаковую частоту, поэтому μ3 = 0, а следовательно, и Аs = 0. Если Аs < 0, то в вариационном ряду преобладают (имеют большую частоту) варианты, которые меньше, чем средняя, т.е. ряд отрицательно асимметричен (или с левосторонней скошенностью – более длинная ветвь влево). Положительная ассиметрия (правосторонняя скошенность – более длинная ветвь вправо) характеризуется значением Аs > 0 (рис. 5.7).
, имеют одинаковую частоту, поэтому μ3 = 0, а следовательно, и Аs = 0. Если Аs < 0, то в вариационном ряду преобладают (имеют большую частоту) варианты, которые меньше, чем средняя, т.е. ряд отрицательно асимметричен (или с левосторонней скошенностью – более длинная ветвь влево). Положительная ассиметрия (правосторонняя скошенность – более длинная ветвь вправо) характеризуется значением Аs > 0 (рис. 5.7).
Аs = 0
 | |||
 | |||
Правосторонняя Левосторонняя
АS > 0 АS < 0
 |
Рис. 5.7. Асимметрия распределения
В качестве показателя асимметрии применяют и коэффициент асимметрии Пирсона (AsП):
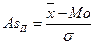 .
.
Показатель Пирсона зависит от степени асимметричности в средней части ряда распределения, а показатель асимметрии, основанный на μ3, - от крайних значений признака.
Если распределение по форме близко к нормальному закону, то медиана находится между модой и средней величиной, причем ближе к средней, чем к моде.
При правосторонней асимметрии 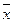 > Ме > Мо.
> Ме > Мо.
При левосторонней асимметрии 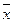 < Ме < Мо.
< Ме < Мо.
Для умеренно асимметричных распределений справедливо равенство: | Мо -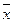 | = 3| Ме -
| = 3| Ме -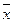 |.
|.
С помощью момента четвертого порядка характеризуется еще более сложное свойство рядов распределения, чем асимметрия, называемое эксцессом. Термин «эксцесс» в переводе означает «излишество».
Отношение 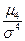 характеризует крутизну (заостренность) графика распределения. Для нормального распределения
характеризует крутизну (заостренность) графика распределения. Для нормального распределения 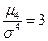 , поэтому для оценки крутизны данного распределения в сравнении с нормальным рассчитывается эксцесс распределения:
, поэтому для оценки крутизны данного распределения в сравнении с нормальным рассчитывается эксцесс распределения:
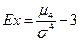 .
.
Наличие положительного эксцесса означает, что в изучаемой массе явлений существует слабо варьирующее по данному признаку «ядро», окруженное рассеянным «гало». При существенном отрицательном эксцессе такого «ядра» нет совсем (рис. 5.8).
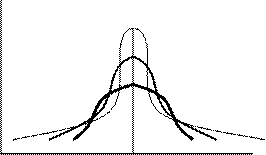 |
Eх >0
Eх =0
Eх <0
Рис. 5.8. Эксцесс распределения
 2014-01-25
2014-01-25 1198
1198

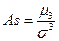 .
.