Свойства функций распределения независимых случайных величин

Зависимые и независимые случайные величины

Замечание 1. Ранее было введено определение независимых случайных величин: две случайных величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Из этого определения следует, что условные распределения независимых случайных величин равны их безусловным распределениям: , .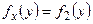

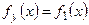Требуется получить необходимые и достаточные условия независимости случайных величин.

Теорема 1. Для того чтобы случайные величины Х и У были независимыми, необходимо и достаточно, чтобы функция распределения системы 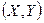была равна произведению функций распределения составляющих: .

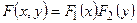Доказательство. 1. Необходимость. Пусть Х и У независимые случайные величины. Тогда события 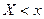и 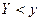независимы, следовательно, вероятность совмещения этих событий равна произведению их вероятностей: 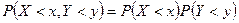или (в силу определения функции распределения) .

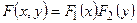2. Достаточность. Пусть .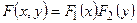

Отсюда 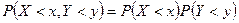, т.е. вероятность совмещения событи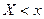й и 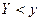равна произведению вероятностей этих событий. Тогда события 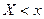и 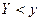, и, следовательно, случайные величины Х и У независимы. Теорема доказана.

Следствие. Для того чтобы непрерывные случайные величины Х и У были независимыми, необходимо и достаточно, чтобы дифференциальная функция распределения системы 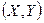была равна произведению дифференциальных функций распределения составляющих: .

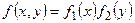Доказательство. 1. Необходимость. Пусть Х и У независимые случайные величины. Тогда (на основании теоремы 1) 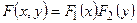. Дифференцируя это равенство по 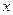, а затем по 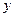, имеем: 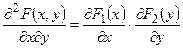. Или (по определению дифференциальных функций двумерной и одномерной случайных величин) .

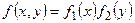2. Достаточность. Пусть 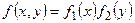. Интегрируя это равенство 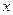по и по 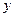, имеем: 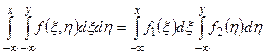. Или (в силу формулы (22.3) и свойств дифференциальной функции распределения одномерной случайной величины) 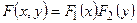, откуда (по теореме 1) следует, что случайные величины Х и У независимы. Следствие доказано.

Замечание 2. Так как теорема 1 и следствие из неё представляют собой необходимые и достаточные условия, то можно дать равносильные определения независимых случайных величин.

Определение 1. Две случайные величины называются независимыми, если функция распределения вероятностей системы этих величин равна произведению интегральных функций составляющих.

Определение 2. Две непрерывные случайные величины называются независимыми, если дифференциальная функция распределения вероятностей системы этих величин равна произведению дифференциальных функций составляющих.

Замечание 3. Можно доказать, что для независимых случайных величин Х и У линии регрессии Н по Х и Х по У параллельны координатным осям Ох и Оу.