Уравнение Клаузиуса (31) можно обобщить на случай, когда система, совершающая циклический процесс, обменивается теплотой не с двумя, а с n источниками, имеющими температуры T 1, T 2,..., Tn. В этом случае (31) заменяется на уравнение
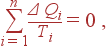
| (34) |
где Δ Qi – количество теплоты, получаемое системой от i -го источника. В случае же, когда система обменивается теплотой с непрерывно распределенными источниками, сумма по n заменяется интегралом, взятым по всему циклу, и уравнение Клаузиуса принимает вид
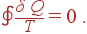
| (35) |
Уравнение Клаузиуса справедливо, если все части цикла представляют собой обратимые процессы и цикл является обратимым. Если же цикл включает в себя необратимый процесс и оказывается необратимым, то уравнение (35) не выполняется и имеет место неравенство Клаузиуса
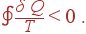
| (36) |
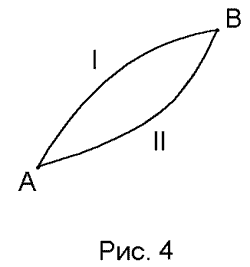
Свойство обратимых циклов, выражаемое уравнением Клаузиуса (35), можно представить в иной форме. Рассмотрим обратимый процесс, при котором система переходит из состояния A в состояние B. Обычно возможно множество различных обратимых процессов, переводящих систему из одного равновесного состояния в другое. Любой непрерывной кривой, соединяющей точки A и B на диаграмме (V, P), соответствует возможный обратимый процесс от A до B.
|
|
|
|
На рис. 1.4 показаны два таких процесса. Рассмотрим цикл AIBIIA, составленный из двух произвольных обратимых процессов I и II, соединяющих точки A и B на рис. 1.4. Поскольку этот цикл является обратимым, то согласно (35)
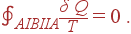
| (37) |
Разобьем интеграл по циклу на сумму двух интегралов, первый из которых берется по пути AIB, а второй – по пути BIIA, т.е. перепишем (37) в форме
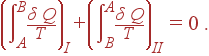
|
Если перенести теперь второй интеграл направо и поменять в нем пределы интегрирования, то получается соотношение
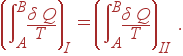
|
Таким образом, интеграл
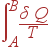
|
зависит только от начального и конечного состояний A и B, но не зависит от самого процесса, т.е. является одним и тем же для всех обратимых процессов от A до B.
Это свойство позволяет ввести новую функцию состояния системы, называемую энтропией, которая представляет собой исключительно важную термодинамическую величину. Энтропией состояния A называется величина
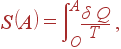
| (38) |
где интеграл берется по произвольному обратимому процессу от состояния O, прнятого за начало отсчета.
Определим разность энтропий в состояниях A и B. Для этого рассмотрим обратимый цикл OBAO. Поскольку цикл обратим, то интеграл
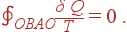
|
Разобьем интеграл по циклу на сумму трех интегралов:
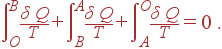
|
Согласно определению (38) первый интеграл представляет энтропию в состоянии B, а третий – энтропию в состоянии A со знаком минус. Отсюда следует, что
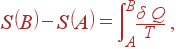
| (39) |
где интеграл берется по произвольному обратимому процессу от A до B.
|
|
|
Формула (38) представляет энтропию с точностью до аддитивной постоянной. Эта неопределенность не проявляется, если нас интересует разность энтропии в различных состояниях (39), которая не зависит от состояния O, принятого за начало отсчета. Однако в некоторых случаях аддитивная константа играет важную роль. Величина ее устанавливается третьим законом термодинамики, о котором речь будет позже.
Если от конечного процесса перейти к бесконечно малому процессу, то (39) принимает вид
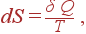
| (40) |
т.е. изменение энтропии при бесконечно малом обратимом процессе равно количеству теплоты δ Q, деленному на температуру системы T.
Формула (40) означает, что отношение δ Q / T является полным дифференциалом, в то время как δ Q не является таковым. Это соотношение представляет следствие постулата Клаузиуса. Поэтому его часто называют вторым законом термодинамики, математическим следствием которого оно и является.
Подставим сооотношение δ Q = TdS в уравнение первого закона термодинамики (9). В результате получаем дифференциальное уравнение
| dE = TdS – PdV, | (41) |
которое называется основным термодинамическим тождеством. Оно объединяет первый и второй законы термодинамики и справедливо для бесконечно малых обратимых процессов.
Энтропия составной системы равна сумме энтропий ее частей. Это верно, если энергия и работа аддитивны, т.е. если энергия системы равна сумме энергий всех ее частей, а работа, совершаемая системой, равна сумме работ, совершаемых ее частями. Энергия системы аддитивна, если можно пренебречь энергией взаимодействия подсистем по сравнению с их энергиями, т.е. если поверхностная энергия мала по сравнению с объемной. Для системы, состоящей из двух различных веществ, это так, если они не очень сильно размельчены. В противном случае поверхностная энергия играет важную роль.
Итак, если система состоит из двух частей и внутренняя энергия и работа аддитивны,
| E = E 1+ E 2, L = L 1+ L 2, |
то поглощаемая системой теплота также аддитивна: Q = Q 1+ Q 2. Это означает, что аддитивна и энтропия:
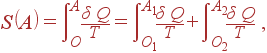
| (42) |
где O 1,2 и A 1,2 обозначают состояния подсистем, когда составная система находится в состояниях O и A соответственно.
Отметим, что выражение (42) можно использовать для определения энтропии системы, не находящейся в состоянии равновесия, если ее можно разбить на части, находящиеся в равновесных состояниях.
Изменение энтропии системы при переходе из состояния A в B определяется уравнением (39), если интеграл берется по обратимому процессу. Если же интеграл берется по необратимому процессу, то равенство (39) нарушается. Чтобы определить изменение энтропии в этом случае, рассмотрим необратимый цикл AIBRA, состоящий из необратимого процесса I от A до B и обратимого процесса R от B до A (рис. 1.5).
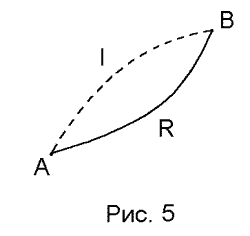
|
Применяя неравенство Клаузиуса (36) к этому циклу, имеем
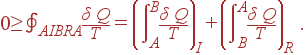
| (43) |
К обратимому процессу R можно применить соотношение (39), согласно которому второе слагаемое в (43) равно разности 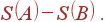 Это приводит к неравенству
Это приводит к неравенству
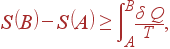
| (44) |
где интеграл берется по произвольному необратимому процессу I от A до B.
 2015-07-03
2015-07-03 458
458







