Формулы работы с процентными ставками

Под наращенной суммой понимают первоначальную ее сумму с начисленными процентами к концу срока.

Для записи формулы наращения простых процентов примем обозначения:

I — проценты за весь срок ссуды;

P — первоначальная сумма долга;

S — наращенная сумма в конце срока;

i — ставка наращения (десятичная дробь) или процентная ставка;

n — срок ссуды (обычно в годах).

Наращенные за весь срок проценты определяются умножением первоначальной суммы долга на множитель наращения, который показывает, во сколько раз наращенная сумма больше первоначальной. Если срок измеряется в годах, то i означает годовую процентную ставку. Соответственно, каждый год приносит проценты в сумме P×i. А начисленные за весь срок проценты составят:

I = P×n×I (1)

Наращенная сумма, таким образом, находится:

S = P + I = P+ P·n·i = P×(1+ n×i) (2)

Формулу (2) называют формулой наращения простых процентов, а (1+ n×i) называют множителем наращения простых процентов.

Поскольку процентная ставка, как правило, устанавливается в расчете за год, то при сроке ссуды менее года необходимо определить, какая часть годового процента уплачивается кредитору. Аналогичная проблема возникает в случаях, когда срок ссуды меньше периода начисления.

Если обозначить:

t — число дней ссуды;

К — число дней в году,

то можно выразить срок ссуды в виде дроби:

n = t / K (3)

При расчете необходимо обеспечить выбор варианта в зависимости от:

1) базы длительности года (К = 360 — обыкновенные или коммерческие проценты и К = 365, 366 дней — точные проценты);

2) базы количества дней в месяце (каждый месяц — 30 дней или учитывается точное число календарных дней);

3) распределения начисления процентов в смежных календарных периодах (общая сумма процентов делится между периодами согласно фактическим датам).

При разработке условий контрактов или их анализе и сравнении возникает необходимость в решении ряда вторичных задач – определение срока ссуды и размера процентной ставки в том или ином виде при всех прочих заданных условиях.

Продолжительность ссуды можно рассчитать, решив (2) относительно n:

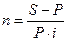(4)

Аналогично можно получить величину процентной ставки:

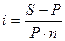(5)

Принципиально ничего не меняется, если сумма, на которую начисляются проценты, изменяет свою величину во времени. В этом случае:

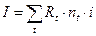, (6)

где R_t – остаток средств на счете в момент t после очередного поступления или списания средств, n_t – срок хранения денег до нового изменения остатка средств на счете.

База для начисления сложных процентов в отличие от простых не остается постоянной – она увеличивается с каждым шагом во времени. В таком случае абсолютная сумма начисляемых процентов возрастает, и процесс увеличения суммы долга происходит с ускорением. Наращение по сложным процентам можно представить как последовательное реинвестирование средств, вложенных под простые проценты на один период начисления. Очевидно, что в конце первого периода проценты равны P·i, а наращенная сумма P +P·i = P·(1+i). К концу второго периода она достигнет величины P·(1+i)+ P·(1+i)·i = P·(1+i)² и т.д. В конце n –го периода наращенная сумма будет равна:

S = P×(1+ i)ⁿ. (7)

Проценты за весь срок ссуды:

I = S – P = P×[(1+ i)ⁿ-1]. (8)

Часть из них получена за счет начисления процентов на проценты. Она составляет:

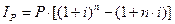. (9)

Очевидно, что рост по сложным процентам представляет собой процесс, соответствующий геометрической прогрессии, первый член которой равен Р, а знаменатель – (1+i). Последний член прогрессии равен наращенной сумме в конце срока ссуды. Величину (1+i)ⁿ называют множителем наращения.

Формула для расчета будущей стоимости серии фиксированных периодических платежей, если они вносятся в начале каждого периода (так называемые «обязательные платежи» или пренумерандо), будет содержать n слагаемых вида (7) и примет вид:

S = P×(1+ i)+ P×(1+ i)² +...+ P×(1+ i)ⁿ = 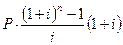. (10)

Здесь количество слагаемых соответствует числу платежных периодов.

Для расчета будущей стоимости серии фиксированных периодических платежей, если выплаты происходят в конце периода (так называемые «обычные платежи» или постнумерандо), формулу (10) следует модифицировать:

S = P+ P×(1+ i) +...+ P×(1+ i)^n-1 = 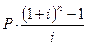. (11)

Предположим теперь, что требуется найти текущую стоимость будущих периодических постоянных платежей, которые производятся в начале или в конце каждого расчетного периода. Согласно концепции временной стоимости, чем дальше отстоит от настоящего момента поступление или расходование средств, тем меньшую текущую ценность оно представляет. Таким образом, при прочих равных условиях текущая стоимость вкладов пренумерандо больше, чем текущая стоимость вкладов постнумерандо.

Необходимо отметить, что основная формула сложных процентов (10) предполагает постоянную процентную ставку на протяжении всего срока начисления процентов. Однако если используют плавающие или переменные процентные ставки, то наращенная сумма рассчитывается так:

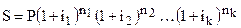, (12)

где i₁, i₂,..., i_k- последовательные во времени значения процентных ставок; n₁, n₂,..., n_k - длительность периодов, в течение которых используются соответствующие ставки.

Операция дисконтирования означает приведение стоимостного показателя, относящегося к будущему, на некоторый, более ранний момент времени. Данная задача является обратной наращению процентов: по величине S определяется Р. В этом случае говорят, что сумма S дисконтируется или учитывается, сам процесс начисления процентов и их удержание называют учетом, а удержанные проценты — дисконтом.

Величину Р, найденную с помощью дисконтирования, называют современной капитализированной стоимостью.

Рассчитаем значение дисконтного множителя и дисконт D с суммы долга S,полученной в формуле (2):

P = S / (I + n×i), (13)

D = S – Р. (14)

Таким образом, решается задача, обратная задаче наращения первоначальной суммы ссуды, а именно: определяется, какую первоначальную сумму надо дать в долг, чтобы получить в конце срока сумму S при условии, что на долг начисляются проценты по ставке i. Дисконтный множитель, равный 1/(1+ n×i), показывает, какую долю составляет первоначальная величина долга в его окончательной сумме.

Аналогичным приемом из формулы (7) можно определить величину дисконтирования по ставке сложных процентов:

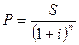. (15)