Политропный процесс

Политропными называются процессы, происходящие при постоянной теплоёмкости и вызываемые подводом тепла к рабочему телу или отводу тепла от него. Политропный процесс подчиняется уравнению: 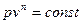, где показатель n может иметь любое значение от - 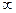до + 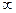, а в зависимости от значения n будет изменяться и характер протекания процессов. Для каждого политропного процесса показатель n ― величина постоянная.

к= 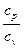― показатель адиабаты.

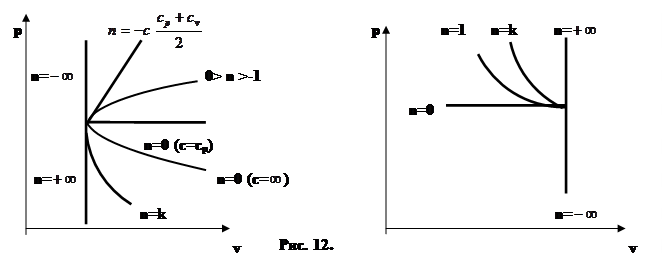
Так как изохорный, изобарный, изотермический и адиабатные процессы являются частным случаем политропного процесса, то докажем это. Уравнение политропного процесса имеет вид: .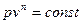

При n=0 получаем р=const, так как v⁰=1, а это – уравнение изобарного процесса.

При n=1 получаем рv=const, а это уравнение изотермического процесса.

При n=k получаем рv^k=сonst, а это – уравнение адиабатного процесса.

При n= 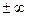уравнение политропы превращается в уравнение v=const, а это уравнение изохорного процесса.