Теорема об изменении кинетической энергии механической системы

Умножим скалярно обе части равенства (2) (левую и правую) на скорость k-той точки системы 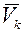и получим:

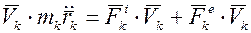умножим обе части на 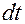, заменив :

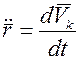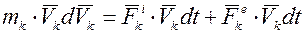, где k=1, 2, 3, …, n (13-а)

так как 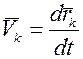то 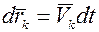, поэтому правую часть равенства (13-а) преобразуем, подставив в нее :

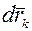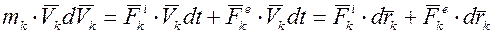(13-б)

Но выражения:

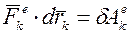(14) - это элементарная работа k-той внешней силы

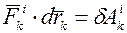(15) - это элементарная работа k-той внутренней силы

Тогда уравнение (13-б) можно записать в виде:

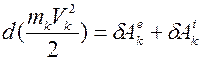, где к=1, 2, 3, … n. (16)

так как, смотри первое из двух уравнений (13-а)

)

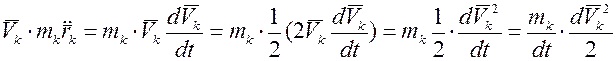т.е.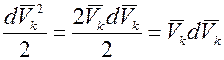

В выражении (16): 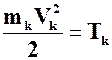(17) - кинетическая энергия k-той точки механической системы, которая является второй мерой механического движения.

В целом кинетическая энергия механической системы (18) равняется сумме кинетических энергий всех n точек:

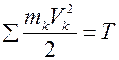(18)

Суммируя уравнение (16) по всем n точкам механической системы, получим:

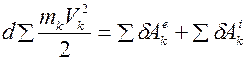(19) где

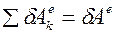- элементарная работа внешних сил, действующих на систему,

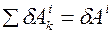- элементарная работа внутренних сил, действующих на систему,

Тогда уравнение (19) можно записать в виде, который называется Теоремой об изменении кинетической энергии механической системы: