Протекание произвольной совокупности элементарных химических процессов в общем случае нельзя описать, используя только одну термодинамическую силу. Тем не менее в некоторых ситуациях с помощью единой термодинамической силы все же возможно описание стационарного протекания стехиометрического брутто-процесса. Простейшим примером являются стехиометрические брутто-процессы, реализующиеся путем произвольной совокупности мономолекулярных элементарных превращений и протекающие в стационарном режиме относительно всех промежуточных компонентов-интермедиатов брутто-процесса. Стационарная скорость такого брутто-процесса оказывается пропорциональной разности термодинамических напоров исходной и конечной реакционных групп. Иными словами, весь такой брутто-процесс с точки зрения кинетики и термодинамики можно рассматривать как одну эффективную элементарную реакцию. Покажем справедливость этого серьезного утверждения на примере простейшей брутто-реакции
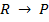 ,
,
где R и Р – исходный реагент и конечный продукт соответственно.
Пусть процесс осуществляется через один интермедиат Y:
s w:val="24"/></w:rPr><m:t>P</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 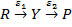
Действительно, в стационарном режиме по интермедиату Y:
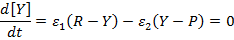
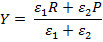
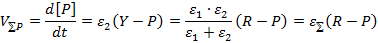
Здесь и далее [A] и A обозначают концентрацию и термодинамический напор реагента А соответственно. Приведенное серьезное утверждение о связи между стационарной скоростью брутто-процесса и вызывающей его термодинамической силой легко обобщить и для случая произвольной совокупности мономолекулярных превращений интермедиатов.
В стационарном режиме химическое брутто-превращение действительно может быть описано единой термодинамической силой. при стационарном протекании химических процессов значения химических потенциалов интермедиатов обязаны находиться между значениями соответствующих величин для исходного реагента и конечного продукта. В стационарном состоянии анализ любого брутто-процесса, состоящего из произвольной совокупности мономолекулярных (или сводимых к ним) превращений, может быть заменен анализом лишь одной эффективной мономолекулярной реакции. Существенно, что этот вывод является общим и справедливым для любой удаленности системы от термодинамического равновесия. Сходные особенности стационарного протекания процесса оказываются характерными и для некоторых брутто-реакций с немономолекулярными промежуточными превращениями. Так, стационарная скорость брутто-процесса пропорциональна разности термодинамических напоров исходной и конечной реакционных групп для любых схем с промежуточными превращениями, линейными по интермедиатам. Однако при этом значение εΣ может зависеть не только от ε ij, но и от термодинамических напоров отдельных исходных или конечных реактантов.
Если реакционная способностьсистемы пребывает в неравновесном состоянии, направление элементарных химических превращений определяется текущими значениями химических потенциалов этих интермедиатов. При этом для стационарного протекания реакции
Значение химических потенциалов (термодинамиеских напоров) всех интермедиатов оказываются жёстко упорядоченными условиями стационарности процесса (рис.1, 2) и описываются выражением
Где -соответсвующая данному промежуточному соединению алгебраическая комбинация величины
, причём
Т.е. зависит только от химических потенциалов (напоров) реагентов и продуктов реакции, а также параметров , которые оределеяются стандартными потенциалами Гиббса образования переходных состояний между разными формами интермедиатов. Поэтому значение стандартных химических потенциалов (напоров) интермедиатов не являются функциями стационарных значений термодинамических (энергетических) характеристик непосредственно самих этих интермедиатов. Интермедиаты «накапливают эергию» исходной реакционной группы, постепенно теря её в ходе превращений в наименее энергоёмкую конечную реакционную группу.
Рис.1. Энергетическая (в координатах химических потенциалов) диаграмма стационарного протекания реакции . (Промежуточные химические превращения осуществляются между стационарными химическими потенциалами
и
, которые являтся функцией параметров
являются функциями стандартных химических потенциалов
только переходных состоний).
Рис.2.Химические потенциаы переходных состояний («горы») и стационарных интермедиатов («озёра») для системы с множественностью путей возможных превращений исходного реагента R в конечный продукт P (уровни стационарных озёр понижаются постепенно от реагента к продукту).
№ 29. В чём разница между элементарными химическими реакциями и брутто-процессами?
Элементарной химической реакцией называют реакцию, которая проходит в одну единственную стадии. Иными словами, элементарная химическая реакция (элементарная стадия) - единичный акт образования или разрыва химической связи при непосредственном взаимодействии частиц (молекул, ионов, радикалов).
Ее можно записать следующим простейшим уравнение:
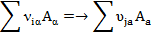
Для этой реакции есть своя собственная константа скорости, показывающая расход вещества (компонента) во времени, а так же своя энергия активации.
Брутто-процесс – это многостадийный процесс, состоящий из множества актов образования/разрыва химических связей при взаимодействии частиц, т.е. это множество элементарных химических реакций.
Брутто-процесс можно представить следующим выражением:
- это произвольная совокупность промежуточных превращений (i, j = 1, …,m), ƐRi и ƐjP – усеченные константы скорости для превращений между группами реагентов R и Ei и P и Ej соответственно.
В отличии от самих элементарных реакций, брутто процесс характеризуется брутто-энергией активации – суммой энергий активации всех частичек, что вступают в элементарный химический акт. Это арениусовская энергия активации (кажущаяся). Так же что касается констант скорости. Брутто-процесс характеризуется множеством констант скоростей, для каждой элементарной реакции по своей, но скорость определяющей является лишь одна – константа скорости лимитирующей стадии.
30. Дать определение термину «скорость-определяющая стадия
По определению ИЮПАК, скорость-определяющей (скорость-контролирующей) стадией в брутто-реакции является элементарная реакция, константа скорости которой производит наибольшее, чем другие константы скорости, влияние на результирующую скорость брутто-реакции.
Формально скорость-контролирующую стадию можно выявить на основе сопоставления значений скорость-контролирующего фактора CFi для разных стадий брутто-процесса:
1) скорость-контролирующий фактор, зависящий от переходных состояний элементарных реакций ij:
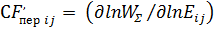 Ekl, μm, kl # ij (k,l,m = 1)
Ekl, μm, kl # ij (k,l,m = 1)
2) скорость-контролирующий фактор, зависящий от стандартных параметров термализованных реактантов Аα:
s w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>О±</m:t></m:r></m:sub><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>o</m:t></m:r></m:sup></m:sSubSup></m:e></m:acc></m:den></m:f></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 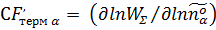 Eij, μβ (β # α),
Eij, μβ (β # α),
где 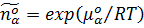 .
.
31. Дать определение термину «скорость-лимитирующая стадия химической реакции
Для сложных реакций суммарная скорость процесса будет связана с характеристиками скорость-контролирующей стадии (скорость-лимитирующая). Скорость-контролирующая стадия, дляреакции протекающей через последовательные элементарные реакции, является та элементарная реакция, константа скорости которой оказывает наиболее сильное влияние на суммарную скорость реакции.
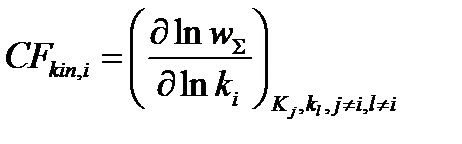 Скорость-контролирующая стадия численно выражается
Скорость-контролирующая стадия численно выражается
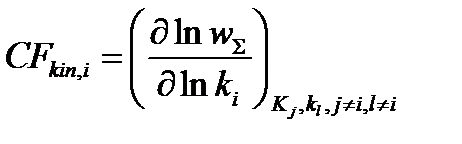
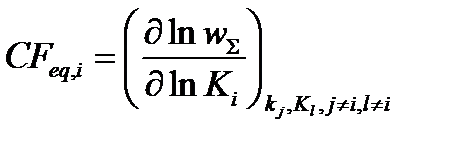 Т.к. для элементарной обратимой реакции константы скорости прямой и обратной реакций равнозначно связаны, то для обратимой реакции величина CF не может быть определена. Поэтому кинетически разделяют стадии на быстрые (кинетически обратимые, которые характеризуются константой равновесия) и медленные (которые характеризуются константой скорости реакции и являются необратимыми). Для каждого случая рассмотрим свой скорость-контролирующий фактор.
Т.к. для элементарной обратимой реакции константы скорости прямой и обратной реакций равнозначно связаны, то для обратимой реакции величина CF не может быть определена. Поэтому кинетически разделяют стадии на быстрые (кинетически обратимые, которые характеризуются константой равновесия) и медленные (которые характеризуются константой скорости реакции и являются необратимыми). Для каждого случая рассмотрим свой скорость-контролирующий фактор.
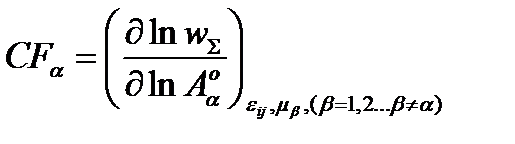
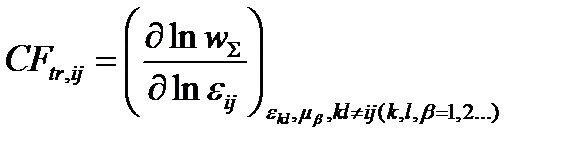 Этот же параметр выражается через термодинамические параметры (усеченную константу скорости, химическое сродство):
Этот же параметр выражается через термодинамические параметры (усеченную константу скорости, химическое сродство):
 Используется для быстрых и медленных реакций, как для обратимых так и для необратимых.
Используется для быстрых и медленных реакций, как для обратимых так и для необратимых.
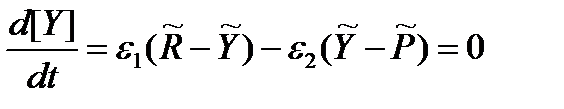
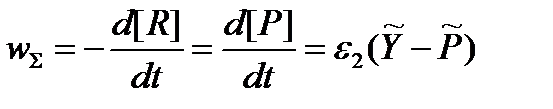
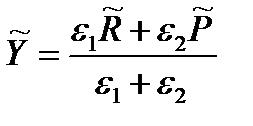
 Критерий выбора скорость-определяющей стадии является минимальное значение усеченной константы скорости.
Критерий выбора скорость-определяющей стадии является минимальное значение усеченной константы скорости.
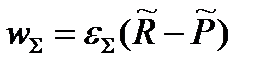
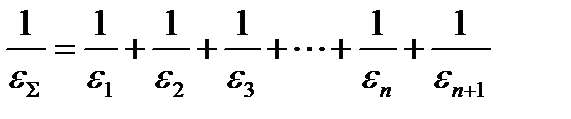
 Еще один критерий выбора скорость-определяющей стадии – максимальное значение термодинамических напоров интермедиатов.
Еще один критерий выбора скорость-определяющей стадии – максимальное значение термодинамических напоров интермедиатов.
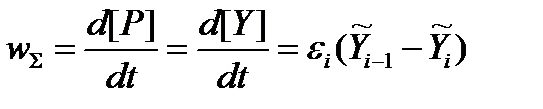
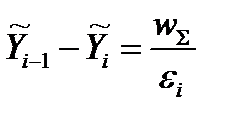
32. УСЛОВИЯ КИНЕТИЧЕСКИ НЕОБРАТИМОЙ РЕАКЦИИ
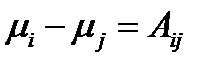
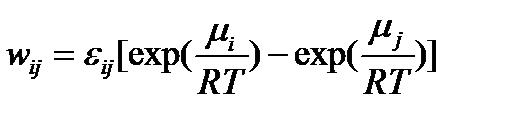
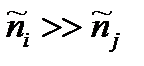
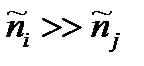 В этом случае будет протекать только прямая реакция
В этом случае будет протекать только прямая реакция
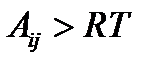
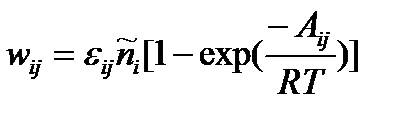
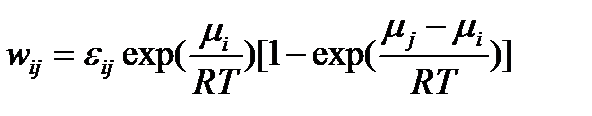
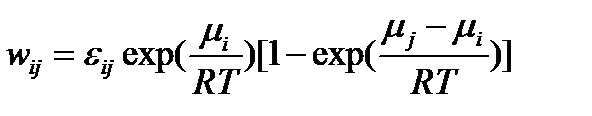 Чем больше абсолютная величина химического сродства прямой реакции, тем более вероятней, что она будет кинетически необратима
Чем больше абсолютная величина химического сродства прямой реакции, тем более вероятней, что она будет кинетически необратима
ИЛИ вариант 2
Совместный кинетико-термодинамический анализ позволяет легко найти корректные термодинамические критерии для широко используемого понятия кинетической необратимости химических реакций. Кинетическая необратимость эквивалентна утверждению, что скорость обратной реакции пренебрежимо мала по сравнению со скоростью той же реакции в прямом направлении.
Очевидно, что для элементарной реакции ij утверждение
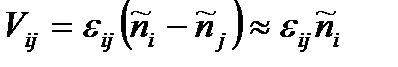 ,
,
эквивалентно ситуации 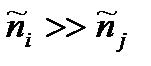 . Поскольку
. Поскольку 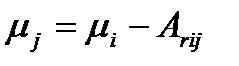 , то
, то
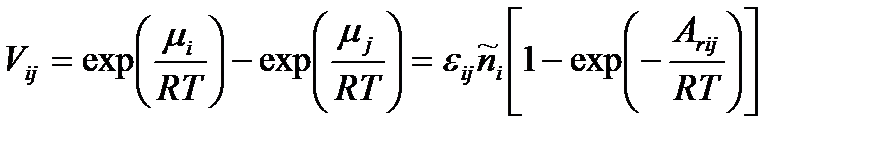 .
.
Поэтому очевидно, что корректным термодинамическим критерием возникновения кинетической необратимости некоторой стадии в цепочке химических превращений является значительное (по сравнению с величиной RT) изменение химического потенциала реакционных групп, соответствующих этой стадии, т. е. 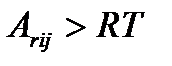 .
.
Для сложной схемы, если известны перепады химических потенциалов на отдельных стадиях, всегда можно осуществить разбиение всей цепочки превращений на кинетически обратимые и кинетически необратимые
Разбиение цепочки последовательных превращений на группы с кинетической «необратимостью» между группами. При протекании реакции «слева направо» превращения 23, 34, 45, 67, 7P могут рассматриваться как кинетические необратимые, в то время как для превращений R1, 12 и 56 всегда необходимо учитывать кинетическую обратимость. Разность между значениями стационарных химических потенциалов промежуточных состояний для первых групп превращений больше RT, в то время как для вторых групп – меньше RT (масштаб указан справа вверху).
Существует условие максимального числа кинетически необратимых стадий (реакций), поскольку в стационарных последовательных химических превращениях полное сродство 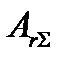 суммарной брутто-реакции равно сумме сродств всех элементарных стадий
суммарной брутто-реакции равно сумме сродств всех элементарных стадий
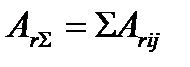 ,
,
то максимальное число кинетически необратимых стадий не может превышать величины 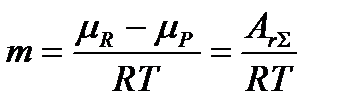 .
.
33. «Энергия активации брутто-процесса»
Для сложного брутто-процесса, который протекает с большим числом промежуточных стадий, суммарная скорость реакции будет определяться лимитирующей стадией, причём эта скорость будет кинетически необратима.
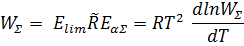
Кажущаяся энергия активации брутто-процесса будет определяться разностью энтальпии образования переходного состояния лимитирующей стадии и энтальпии образования реагентов.
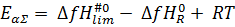 ,
,
где 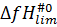 и
и 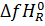 стандартные энтальпии образования переходного состояния скорость-контролирующей элементарной реакции и исходного реагента R соответственно. Иными словами, результирующую энергию активации брутто-процесса определяет разность стандартной энтальпии «наивысшего» по энергии Гиббса переходного состояния и стандартной энтальпии исходного реагента.
стандартные энтальпии образования переходного состояния скорость-контролирующей элементарной реакции и исходного реагента R соответственно. Иными словами, результирующую энергию активации брутто-процесса определяет разность стандартной энтальпии «наивысшего» по энергии Гиббса переходного состояния и стандартной энтальпии исходного реагента.
Данное выражение соответствует правилу, согласно которому кажущаяся энергия активации последовательного процесса равна энергии активации скорость-определяющей стадии минус сумма теплот (или плюс сумма стандартных энтальпий) предыдущих стадий, считающихся равновесными.
Следовательно:
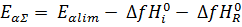
Энергия активации будет равна энергии лимитирующей стадии плюс энтальпии реакции всех предыдущих обратимых стадий:
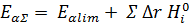
34. взаимодействие между потоком и термодинамической силой вблизи термодинамического равновесия
Вблизи термодинамического равновесия, когда движущие силы весьма малы, а сами процессы протекают достаточно медленно, величины термодинамических сил X и сопряженных с ними потоков J связаны простым линейным соотношением
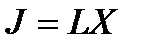 ,
,
где L – некоторый коэффициент, не зависящий от значения термодинамической силыX. Обычно термодинамическиесилы – это градиенты интенсивных термодинамических параметров.
Справедливость линейных отношений типа 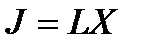 подтверждает, например, закон Ома, где значение потока электричества
подтверждает, например, закон Ома, где значение потока электричества 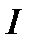 пропорционально движущей силе – разности (градиенту) электрических потенциалов
пропорционально движущей силе – разности (градиенту) электрических потенциалов 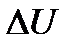 :
:
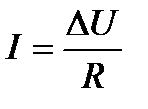 .
.
Таким образом, для данного случая коэффициент пропорциональности 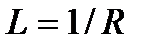 и не зависит от
и не зависит от 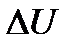 .
.
Аналогичные линейные соотношения между скоростью процесса и движущей силой справедливы и в случае простой диффузии веществ или переноса теплоты за счет теплопроводности.
Так, по закону Фика
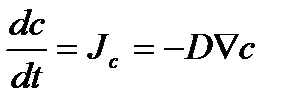 ,
,
т. е., действительно
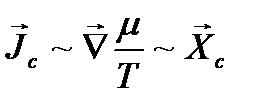 .
.
По закону Фурье
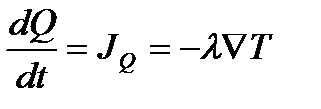 ,
,
т. е., 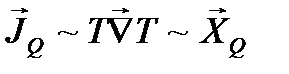 .
.
Здесь  – концентрация диффундирующего вещества,
– концентрация диффундирующего вещества, 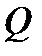 – количество переносимой теплоты, а коэффициенты
– количество переносимой теплоты, а коэффициенты 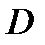 и
и 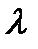 не зависят от градиентов величин
не зависят от градиентов величин  и
и 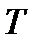 .
.
Вблизи термодинамического равновесия сходные линейные соотношения имеют место и для элементарных химических процессов, а также брутто-процессов, скорость которых пропорциональна разности термодинамических напоров исходной и конечной группы. Критерием близости к термодинамическому равновесию здесь является соотношение 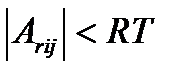 , где
, где 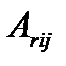 - сродство для превращения реакционной группы i в реакционную группу j.
- сродство для превращения реакционной группы i в реакционную группу j.
Действительно, поскольку
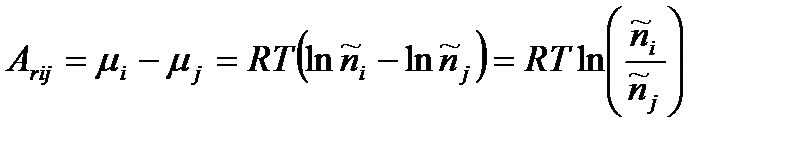 ,
,
то
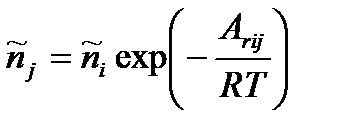
и
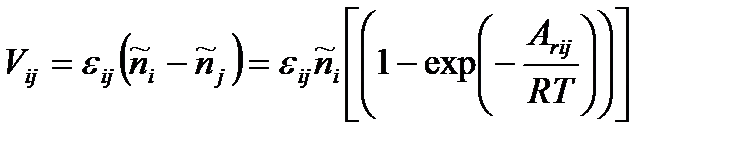 .
.
При 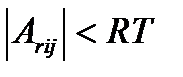 , действительно,
, действительно,
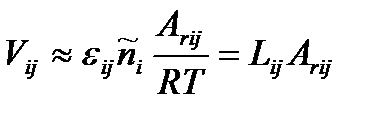 ,
,
где 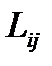 - величина, определяемая равновесным состоянием системы и поэтому не зависящая от значения химического сродства
- величина, определяемая равновесным состоянием системы и поэтому не зависящая от значения химического сродства 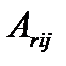 , т. е. термодинамической силы реакции.
, т. е. термодинамической силы реакции.
Очевидно, что вывод о пропорциональности между скоростью реакции и ее химическим сродством справедлив и в ситуации, когда вблизи термодинамического равновесия рассматривается не элементарная, но произвольная сложная стехиометрическая брутто-реакция, которой можно приписать определенное значение химического сродства.
35. Соотношение Онзагера
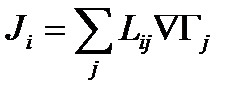 Если в системе протекают несколько процессов, то они способны взаимодействовать между собой. Скорость каждого будет зависеть от движущих сил всех процессов – принцип взаимодействия термодинамических процессов.
Если в системе протекают несколько процессов, то они способны взаимодействовать между собой. Скорость каждого будет зависеть от движущих сил всех процессов – принцип взаимодействия термодинамических процессов.
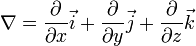
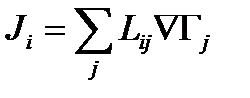
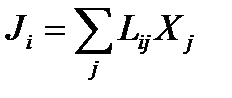
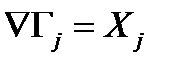
- линейное феноменологическое уравнение взаимности Онзагера
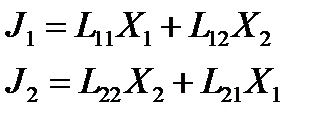 Если протекают два параллельных процесса, то выражение для потоков
Если протекают два параллельных процесса, то выражение для потоков
L12, L21 - коэф. взаимности Онзагера
Обычно коэффициенты равны Lij = Lji - соотношение взаимности Онзагера
Если поток необратимого процесса i испытывает влияние термодинамической силы Хj необратимого процесса j через коэффициенты Lij, то и поток процесса j также испытывает влияние термодинамической силы Хi через тот же самый коэффициент Lij.
Если поток необратимого процесса i испытывает влияние термодинамической силы Хj необратимого процесса j через коэффициенты Lij, то и поток процесса j также испытывает влияние термодинамической силы Хi через тот же самый коэффициент Lij.
 2015-07-02
2015-07-02 1259
1259








