Хорошо известным следствием уравнений Кирхгофа является то, что электрический потенциал в каждой промежуточной точке i описывается выражением
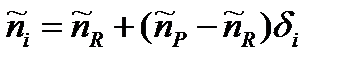
При стационарном протекании химических процессов значения химических потенциалов интермедиатов обязаны находиться между значениями соответствующих величин для исходного реагента и конечного продукта.
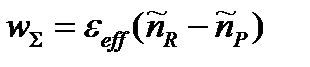
Формула Хориути-Боречкова
Можно сделать вывод что Стационарная скорость сложной реакции, составленной из совокупности мономолекулярных превращений, не зависит от стандартных значений термодинамических параметров интермедиатов и определяется только разностью термодинамических напоров реагента и продукта, а также термодинамическими параметрами переходных состояний между различными интермедиатами
№ 21. Охарактеризуйте термодинамический поток для системы с элементарной химической реакцией.
Перед описание термодинамического потока в таком случае рассмотрим и само понятие потока.
Локальная скорость производства энтропии в единичном объеме определяется соотношением:
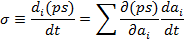
где s - локальная энтропия, отнесенная к единице массы вещества (плотность распределения энтропии), ρ – плотность вещества в данной точке системы, аi – локальное значение макроскопического термодинамического параметра.
По определению величина 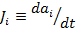 т.е. скорость изменение параметра аi, называется термодинамическим потоком параметра аi (процесса, характеризующегося параметрами аi).
т.е. скорость изменение параметра аi, называется термодинамическим потоком параметра аi (процесса, характеризующегося параметрами аi).
Рассмотрим термически инициированную элементарную химическую реакцию ij вида:
s w:val="24"/></w:rPr><m:t>a</m:t></m:r></m:sub></m:sSub></m:e></m:nary></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 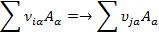
Принято считать, что абсолютная скорость 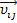 этой реакции ij, т.е. число актов превращений группы реагентов i в группу реагентов j в единице объема и в единицу времени при протекании реакции при заданных температуре и давлении и сохранении распределения Больцмана в заселенности энергетических уровней переходного состояния (активированного комплекса) описывается законом действующих масс:
этой реакции ij, т.е. число актов превращений группы реагентов i в группу реагентов j в единице объема и в единицу времени при протекании реакции при заданных температуре и давлении и сохранении распределения Больцмана в заселенности энергетических уровней переходного состояния (активированного комплекса) описывается законом действующих масс:
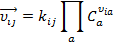
Учитывая, что в общем случаем 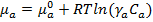 , где
, где 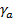 – коэффициент активности вещества α, при этом:
– коэффициент активности вещества α, при этом:
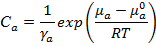
Подставим все значения в закон действующих масс:
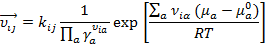
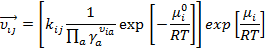
Заменим 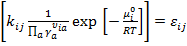 и
и 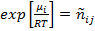 .
.
Получаем, что скорость элементарной химической реакции любого порядка можно записать в виде выражения:
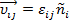
где 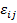 – усеченная константа скорости,
– усеченная константа скорости, 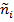 - абсолютная активность компонентов.
- абсолютная активность компонентов.
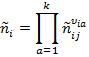
22. Охарактеризовать термодинамическую силу для систем с элементарной химической реакцией

№ 23. Охарактеризуйте термодинамический поток для системы с элементарной обратимой реакцией.
Рассмотрим произвольную элементарную химическую реакцию ij с учетом ее обязательной обратимости:
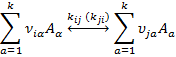
Описывать эту реакцию естественно с помощью «химической переменной» 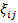 , характеризующей глубину реакции. При этом полная скорость данной реакции, учитывающая и прямой, и обратный процессы, определяется как
, характеризующей глубину реакции. При этом полная скорость данной реакции, учитывающая и прямой, и обратный процессы, определяется как 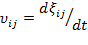 и соответствует разности чисел актов химических превращений в прямом и обратном направлении в единице объема и в единицу времени:
и соответствует разности чисел актов химических превращений в прямом и обратном направлении в единице объема и в единицу времени:
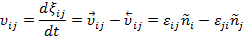
Поскольку для всех элементарных реакций, подчиняющихся правилу детальной обратимости и детального равновесия, 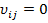 при
при 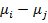 или, что то же, при
или, что то же, при 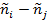 , то с необходимость
, то с необходимость 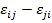 и как следствие
и как следствие
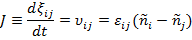
Это выражение имеет наглядный физический смысл и показывает направление химического процесса в зависимости от соотношения величин 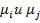 . В силу этого величину
. В силу этого величину 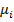 удобно называть термодинамическим напором i-й реакции. Существенно, что разность логарифмов напоров
удобно называть термодинамическим напором i-й реакции. Существенно, что разность логарифмов напоров 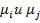 (равная логарифму отношения напоров), умноженная на величину RT, является не чем иным, как текущим термодинамическим сродством
(равная логарифму отношения напоров), умноженная на величину RT, является не чем иным, как текущим термодинамическим сродством 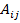 реакции между реакционными группами i и j, т.е. термодинамической силой
реакции между реакционными группами i и j, т.е. термодинамической силой 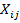 , отвечающей потоку
, отвечающей потоку 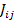 :
:
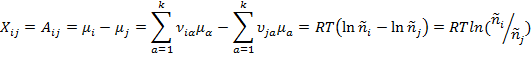
При 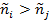 процесс протекает слева направо, при обратном соотношении – справа налево. Эти условия эквивалентны наличию положительного сродства реакции для заданного направления самопроизвольного превращения.
процесс протекает слева направо, при обратном соотношении – справа налево. Эти условия эквивалентны наличию положительного сродства реакции для заданного направления самопроизвольного превращения.
Используя выражение для 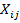 , можно переписать:
, можно переписать:
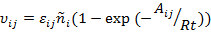
В случае равенства термодинамических напоров 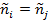 для всех возможных в системе реакций ij система находиться в состоянии устойчивого термодинамического равновесия и поэтому суммарная скорость всех возможных реакции равна 0.
для всех возможных в системе реакций ij система находиться в состоянии устойчивого термодинамического равновесия и поэтому суммарная скорость всех возможных реакции равна 0.
Термодинамический поток 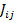 параметра
параметра 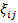 по определению равен скорости реакции, поэтому может быть выражен в виде:
по определению равен скорости реакции, поэтому может быть выражен в виде:
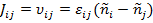
Термодинамическая сила 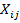 , как выведено ранее, равна:
, как выведено ранее, равна:
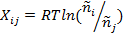
Очевидно, что скорость производства энтропии по каналу элементарной термически инициированной реакции ij в единице объема рассматриваемой системы равна:
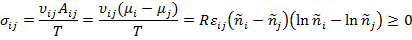
где 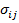 отвечает условию
отвечает условию 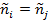 .
.
В случае если обсуждается поток не по химической переменной 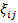 , а по концентрации химического компонента α, то рассматриваемая элементарная реакция дает только одну из составляющих этого потока:
, а по концентрации химического компонента α, то рассматриваемая элементарная реакция дает только одну из составляющих этого потока:
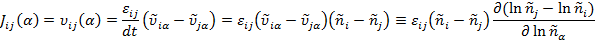
Как видно, при протекании в системе сразу нескольких реакций поток по концентрации компонента в общем случае зависит от многих термодинамических сил. При этом в системе с большим набором термически инициированных элементарных реакций полная скорость производства энтропии в единице объема оказывается равной:
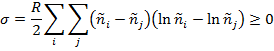
 2015-07-02
2015-07-02 351
351








