Занятие №17. Решение неравенств.
Рассмотрим решение неравенств второй степени. Общий вид таких неравенств: 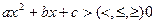
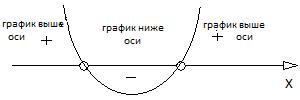
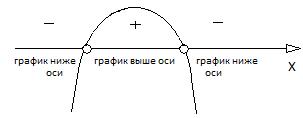
Решение графическим методом: Пусть 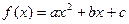 , графиком данной функции является парабола, направление ветвей которой зависит от знака коэф. при
, графиком данной функции является парабола, направление ветвей которой зависит от знака коэф. при 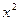 (если a>0 вверх, если a<0 вниз). Найдем точки пересечения графика функции с Ох, т.е. найдем корни уравнения
(если a>0 вверх, если a<0 вниз). Найдем точки пересечения графика функции с Ох, т.е. найдем корни уравнения 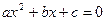 . Схематично построим график учитывая направления ветвей и выберем интервалы соответствующие знаку неравенства.
. Схематично построим график учитывая направления ветвей и выберем интервалы соответствующие знаку неравенства.
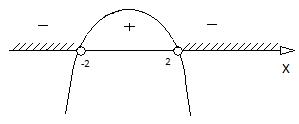 Пример.
Пример. 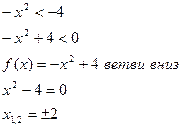
Отв.: 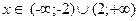
Решение методом интервалов:
1. неравенство приводится к виду: 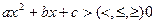
2. находятся корни уравнения 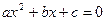
3. на числовой оси обозначаются корни (в зависимости от знака неравенства закрашенные или нет), которые разбивают всю числовую ось на интервалы:
4. определяется знак выражения на каждом интервале. Для этого из каждого интервала выбирается число и подставляется в выражение.
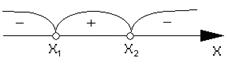
5. выбираются интервалы, знак которых совпадает с требуемым.
Пример. 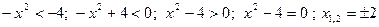
На каждом интервале выбираем число и подставляем в последнее неравенство, стоящее перед уравнением, и определяем знаки на интервалах. Заштриховываем интервалы с нужным знаком:
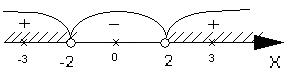
Отв.: 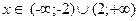
Решить неравенства:
1) 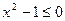 5)
5) 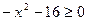
2) 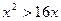 6)
6) 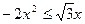
3) 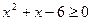 7)
7) 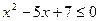
4) 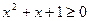 8)
8) 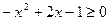
Решить неравенства:
1) 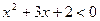
2) 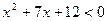
3) 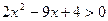
4) 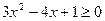
5) 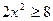
6) 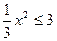
7) 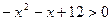
8) 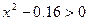
Решить неравенство:
1) 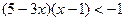 ; 2)
; 2) 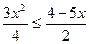 ; 3)
; 3) 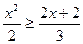 ;
;
При каких значениях x имеет смысл выражение:
1) 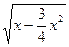 ; 2)
; 2) 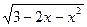 ;
;
Домашнее задание:
Решить неравенства:
1) 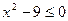 5)
5) 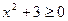
2) 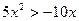 6)
6) 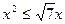
3) 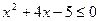 7)
7) 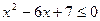
4) 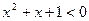 8)
8) 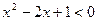
Решить неравенство:
1) 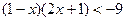 ; 2)
; 2) 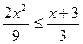 ; 3)
; 3) 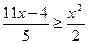 ;
;
При каких значениях x имеет смысл выражение:
1) 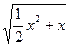 ; 2)
; 2) 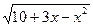 ;
;
 2015-07-03
2015-07-03 624
624







