Решение неравенств вида 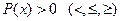 и
и 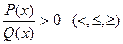 . Такие неравенства решаются методом интервалов.
. Такие неравенства решаются методом интервалов.
Алгоритм решения: 1. ищутся корни знаменателя (корни уравнения 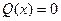 )
)
2. ищутся корни числителя (корни уравнения 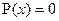 )
)
3. корни числителя и знаменателя отмечаются на числовой оси (корни знаменателя всегда пустыми точками, а корни числителя в зависимости от знака неравенства: строгое - пустые, нестрогое - полные)
4. на каждом интервале определяется знак.
5. выбираются интервалы соответствующие знаку неравенства.
Пример. 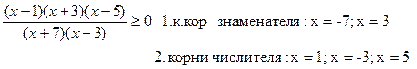

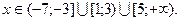
Решить неравенства:
1) 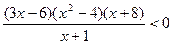 ; 2)
; 2) 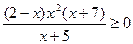 ;
;
3) 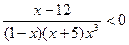 ; 4)
; 4) 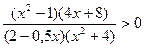 ;
;
5) 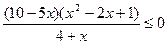 ; 6)
; 6) 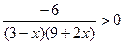 .
.
Решить неравенства:
1) 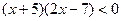 ;
;
2) 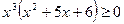 ;
;
3) 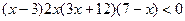 .
.
Дополнительные задания:
Решить неравенства:
1) 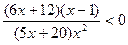 ;
;
2) 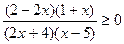 .
.
Домашнее задание:
1) Решить неравенства:
а) 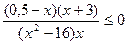 ;
;
б) 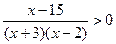 ;
;
в) 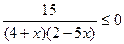 .
.
Решить неравенства:
1) 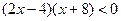 ;
;
2) 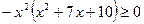 ;
;
3) 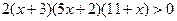 .
.
 2015-07-03
2015-07-03 312
312







