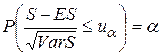 , (13)
, (13)
где
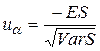 - (14)
- (14)
квантиль нормального распределения.
Решив уравнение (16) относительно неизвестной 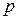 , можем найти как полную премию (брутто-премию)
, можем найти как полную премию (брутто-премию) 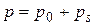 , так и относительную страховую надбавку
, так и относительную страховую надбавку
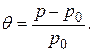
Рассмотрим, например, 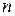 - летнее смешанное страхование жизни.
- летнее смешанное страхование жизни.
4.2. n – летнее смешанное страхование
При этом виде страхования премии вносятся в начале каждого года в течение (не более) n лет, а страховое возмещение выплачивается в конце последнего года жизни.
В случае аппроксимации нормальным приближением, искомую полную периодическую премию можем найти из равенства (14). Предположим, что портфель компании состоит из 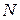 одинаковых договоров смешанного страхования жизни. Тогда:
одинаковых договоров смешанного страхования жизни. Тогда:
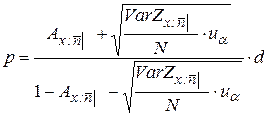 . (15)
. (15)
Здесь

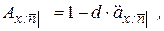
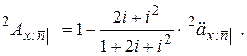 (16)
(16)
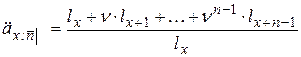 ,
,
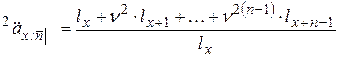 . (17)
. (17)
№ 24. Страховая компания заключила 5000 договоров пятилетнего смешанного страхования с выплатой страховых премий в начале каждого года жизни. Найдите полную нетто-премию, если возраст всех застрахованных равен 30 годам, вероятность неразорения равна 95%, годовая процентная ставка – 20%.
Решение. Применим формулу (15), в которой:
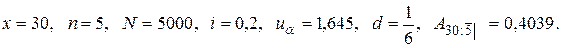
Вычислим дисперсию 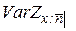 , для чего найдем сначала
, для чего найдем сначала
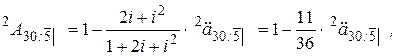
где
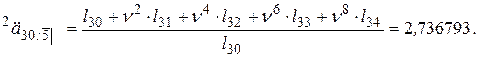
Тогда 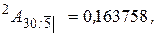
И 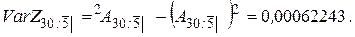
Следовательно,
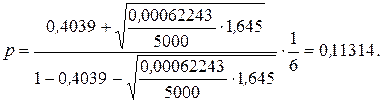
 2015-07-04
2015-07-04 394
394








