2015-07-04
327
Если размерами тела пренебречь нельзя, то оно находится в равновесии, если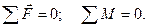 
M = Fd.
III. ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИЧЕСКИХ ПРОЦЕССАХ.
1.Закон сохранения импульса. Импульс тела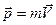 
. Для тела 
; 
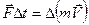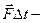импульс силы, 
= 
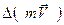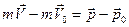- изменение импульса тела.
Для замкнутой системы: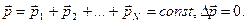 
Для 2-х тел замкнутой системы: 
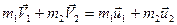
2 .Механическая работа – процесс. Если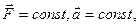 
A = F ∆х Cos α = Fх∆х = F S Cos α, (α – угол между 
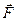и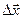 
). На графике F(∆x) и N(t)
если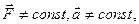 
А = Fср.∆х Cos α = Fср. S Cos α А -площадь
Ag = mg(h1- h2), не зависит от формы траектории.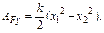 
фигуры.
Мощность.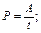 
если 
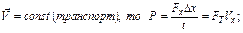К.П.Д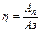 
.
Если V ≠ const, то Рср = Fх Vср.
3. Механическая энергия. Работа – мера изменения энергии. А = Е2 – Е1 = ∆Е.
Потенциальная энергия. Еn = mgh (тело-земля); нулевой уровень-поверхность Земли. En=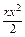 
(деформированная пружина) Кинетическая энергия 
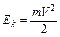(для скоростей V <<c).
Полная механическая энергия тела: Е = Еn max =Еk max = Еn + Еk.
Закон сохранения энергии для замкнутой системы тел:а) Если Fc = 0, то полная энергия системы Е = Е1+Е2+…+ЕN=const; ∆Е = 0.
б) Если Fc ≠ 0, то ∆Е = AFсопр.= (Ек + Еп) – (Еко + Епо),,,
4. Теоремы. Аg = Еп1 –Еп2 = - ∆Еn = -(Еn2 – Еn1); A = ∆Еk = Еk2 – Еk1.
1V. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ.
Уравнение гармонических колебаний: а = - ωо2 х; х =АCos(ω0t+α0); х = АSin(ω0t+α0);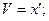 
.
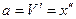Фаза: α = ω0t + α0 ; ω0 – циклическая частота, характеризует колебательную систему (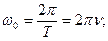
), α о – начальная фаза колебаний.
Математический маятник: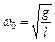 
; 
; 
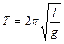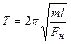-Fн –натяж. нити в полож. равн. в сост покоя. Груз на пружине: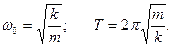 
Закон сохранения энергии: Е = Еk maх = Еn maх = Еn + Еk. E ~ A2.
Волны. λ = VT;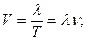 
Уравнение волны: 
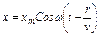, r-расстояние от источника до точки среды, v - c корость волны.
Звуковые волны. Интенсивность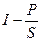 
; порог слышимости: I o = 10 -12 
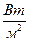. Уровень интенсивности звука: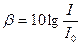 
Сдвиг фаз: ∆α = α2 – α1 или решать пропорцию: λ ÷ 2π (длина волны соответствует разности фаз 2π), а
l ÷ ∆α (расстояние между точками в волне соответствует разности фаз ∆α)
