А) Выражение переменных и подстановка их в целевую функцию

Для этого выражают m компонент (переменных) вектора Х через остальные (n-m) и подставляют в целевую функцию. Таким образом, получают задачу на безусловный экстремум целевой функции.

Пример 10. Найти экстремум функции Z(X) = 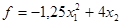при условии:

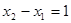
Решение. Из ограничения (уравнения условия или уравнения связи) выразим х₂ через х₁ и подставим полученное выражение в функцию Z(X) = f.

х₂ = х₁ + 1

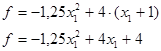
Геометрически данная функция представляет собой параболу, ветви которой направлены вниз, т.к. а = -1,25< 0. Вершина параболы, в которой достигается максимум функции, находится в точке с координатами 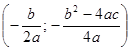. Найдем координаты искомой точки: .

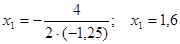Тогда х₂ = 1,6 + 1; х₂ = 2,6

Таким образом, точкой условного экстремума (максимума) функции Z(X) = 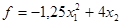при условии 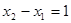является точка Х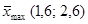^* = и Z(X^*) = .

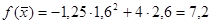Описанный выше подход применим не ко всем задачам, так как не всегда легко выразить переменные из уравнений связи и исследовать полученную функцию. Более универсальным методом решения задач на нахождение условного экстремума является метод множителей Лагранжа.