Метод штрафных функций

Штрафная функция – это взвешенная сумма квадратов невязок, т.е. штраф за невыполнение ограничений. Задача с ограничениями в этом случае сводится к задаче без ограничений.

Алгоритм решения задач выпуклого программирования методом штрафных функций при решении задачи на минимум целевой функции

Решить задачу выпуклого программирования

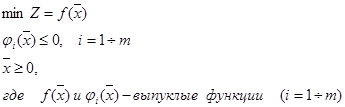
1. Находим область допустимых решений w, т.е. нижнюю и верхнюю границы изменения переменной. Подготавливаем начальный вектор

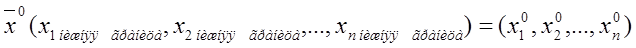
координатами которого служат нижние границы изменения координат из области допустимых решений w. Задаем число М для задания функции штрафов. Например, М=100. Формируем массив случайных чисел 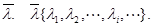Вводим счетчик S=0 – счетчик неудачных попыток.

2. Находим функцию штрафов

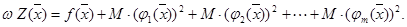
Выражение в круглых скобках – штрафы за невыполнение ограничений.

3. Вычисляем функцию штрафов в точке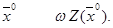

4. Формируем случайный вектор , где Î w, координаты которого вычисляются по правилу ,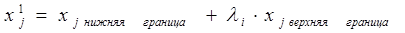

где l_i – число из массива случайных чисел.

5. Находим функцию штрафов в точке .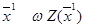

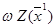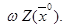6. Сравниваем и Если 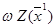≤ 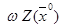, то испытание удачное и переходим к пункту 7, иначе переход к пункту 8.

7. Начальному вектору 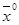придаем значение ( 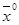= ) и полагаем штраф = .

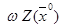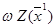Переход к пункту 4.

8. Если 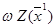> 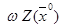, то вектор 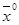и штраф 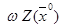остаются прежними, но ведем счет неудавшихся попыток S = S + 1.

9. Если S ≤ N, где N – контрольное число, например, N=1000, то переходим к пункту. Иначе переход к пункту 10.

10. Конец вычислений. Запись ответа координат вектора 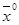и штрафа .

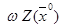Замечание. При больших значениях М (М®¥) 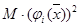®0, т.е. штраф 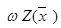стремится к значению целевой функции. 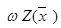® 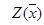, а

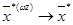. Параметр М в процессе решения может меняться от малой величины до большой.

При решении задачи на максимум целевой функции штраф равен

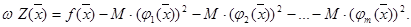
Пример 19

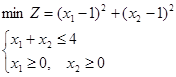
1. Находим область допустимых решений w:

0 ≤ х₁ ≤ 4 х₁⁰ = х_{1 нижняя граница} = 0;

0 ≤ х₂ ≤ 4 х₂⁰ = х_{2 нижняя граница} = 0;

М = 10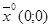

Выпишем массив случайных чисел 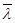: 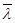(0,44; 0,19; 0,36; 0,91; 0,25; 0,31; 0,11; 0,14; 0,17; 0,24; 0,16; 0,47; …).

S = 0 – счетчик неудачных попыток.

2. Формируем функцию штрафов:

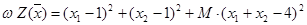
3. Вычисляем функцию штрафов в точке 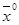(0;0).

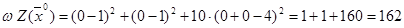
4. Формируем случайный вектор :

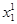= х_{1 нижняя граница}+ l_j·х_{1 верхняя граница}

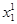= 0+0,44 · 4 = 1,76

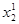= х_{2 нижняя граница}+ l₂·х_{2 верхняя граница}

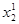= 0+ 0,19· 4 = 0,76

(1,76; 0,76) Îw

5. Вычисляем функцию штрафов в точке :

w Z() = (1,76 – 1)² + (0,76 – 1)² + 10 · (1,76 + 0,76 – 4)² = (0,76)² +

+ (-0,24)² + 10 · (1,48)² =0,5776 + 0,0576 +20,904 = 21,5392

6. Сравниваем w Z() и :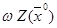

21,5392 < 162. Испытание удачное.

7. Начальному вектору 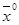придаем значение , т.е. 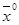(1,76; 0,76).

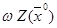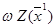= = 21,5392.

8. Формируем новый случайный вектор :

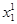= 0+ 0,36 · 4 = 1,44

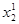= 0 + 0,91 · 4 = 3,64

(1,44; 3,64) Ï w, т.к. 1,44 + 3,64 = 5,08, а по условию х₁ + х₂ ≤ 4.

5,08 > 4.

9. Формируем случайный вектор :

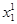= 0 + 0,25· 4 =1

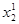= 0 + 0,31 · 4 = 1,24

(1; 1,24) Î w

10. Вычисляем функцию штрафов в точке :

w Z() = (1 – 1)² + (1,24 – 1)² + 10 · (1 + 1,24 – 4)² = 0² +

+ (0,24)² + 10 · (1,76)² =0 + 0,0576 +30,946 = 31,0036.

11. Сравниваем w Z() и :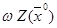

31,0036 > 21,5392. Испытание неудачное.

12. Ведем счет неудавшихся попыток: S = S + 1; S = 0 + 1; S = 1.

13. S < 3, где 3 – контрольное число неудачных попыток для ручного счета.

14. Формируем новый случайный вектор :

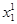= 0 + 0,11 · 4 =0,44

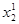= 0 + 0,14 · 4 = 0,56

(0,44; 0,56) Î w

15. Вычисляем функцию штрафов в точке :

w Z() = (0,44 – 1)² + (0,56 – 1)² + 10 · (0,44 + 0,56 – 4)² =(0,56)² +

+ (0,44)² + 10 · (3)² =0,3136 + 0,1936 +90 = 90,5072.

16. Сравниваем w Z() и :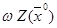

90,5072 > 21,5392. Испытание неудачное.

17. Ведем счет неудавшихся попыток: S = S + 1; S = 1 + 1; S = 2.

18. S < 3, где 3 – контрольное число неудачных попыток для ручного счета.

19. Формируем новый случайный вектор :

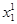= 0 + 0,17 · 4 =0,68

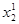= 0 + 0,24 · 4 = 0,96

(0,68; 0,96) Î w

20. Вычисляем функцию штрафов:

w Z() = (0,68 – 1)² + (0,96 – 1)² + 10 · (0,68 + 0,96 – 4)² =(0,32)² +

+ (0,04)² + 10 · (2,36)² =0,1024 + 0,0016 +55,696 = 55,8.

21. Сравниваем w Z() и :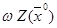

55,8 > 21,5392. Испытание неудачное.

22. Ведем счет неудавшихся попыток: S = S + 1; S = 2 + 1; S = 3.

23. S = 3, где 3 – контрольное число неудачных попыток для ручного счета. Следовательно, испытание прекращаем и выписываем ответ:

X* = 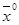(1,76; 0,76); min Z =21,5392.

Пример 20

min Z=9x₁²+9x₂²+12x₁-6x₂

0≤x≤4

1≤ x₂≤5

Изобразим решение на графике.

Для этого преобразуем целевую функцию:

Z=9x₁²+12x₁+9x₂²-6x₂ = 9(x₁²+ 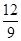x₁) + 9(x₂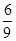²- x₂₎;

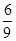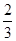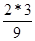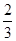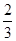Z = 9(x₁²+2· x₁+())+9(x₂²- x₂)= 9(x₁²+2· x₁+())+9(x₂²- 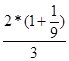x₂) - - 9· - ;

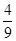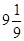Z = 9(x₁+ 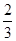)²+9(x₂- 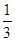)²-4-1==9(x₁+ 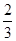)²+9(x₂- 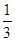)²-5

C₁₁=C₂₂=9 ─ линии уровня концентрические окружности с центром в точке O₁(; ).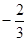

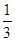Min Z=3 в оптимальном решении точке Х*(0;1).

Формируем начальный вектор 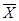⁰:

x₁^{0 =X}_{1 нижняя граница} =0;

x₂^{0 =X}_{2 нижняя граница} =1.

Тогда 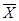⁰(0;1) – нижняя граница координат.

2. Пусть M = 0,01, N=3 –число неудачных испытаний для ручного счета.

Массив случайных чисел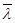

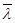(0,44;0,19;0,36;0,91;0,25;0,31;0,11;0,14;0,17;0,24;0,16;0,47…)

S= 0 - счетчик неудачных испытаний

3. Вычислим Z ( 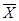⁰)= Z(0,1)=12-6=3

4. Вычисляем функцию штрафов

WZ(x) = f(x)+М(φ₁( 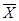))²+M(φ₂( 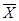))²+…+ M(φ_m(_X))²

5. Вычисляем функцию штрафов в точке 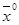(0;0).

WZ( 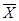⁰) = 9x₁²+9x₂²+12x₁- 6x₂+0,01(x₁-4)²+0,01(x₂-5)² +0,01(1-x₂)²

WZ( 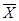⁰) = 3+0,01·16+0,01·16 +0,01·0 = 3,32.

6. Формируем случайный вектор :

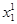= х_{1 нижняя граница}+ l_j·х_{1 верхняя граница}

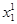= 0+0,44 · 4 = 1,76

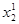= х_{2 нижняя граница}+ l2·х_{2 верхняя граница}

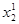= 1+ 0,19· 5 = 1,95

(1,76; 1,95) Îw

5. Вычисляем функцию штрафов в точке :

wZ() = 9(1,76)² + 9(1,95)² + 12·1,76-6·1,95+0,01 · (1,76 – 4)² +0,01 · (1,95 –5)² +0,01 · (1-1,95)² = 71,66224.

11. Сравниваем wZ() и :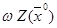

71,66224 > 3,32. Испытание неудачное.

12. Ведем счет неудавшихся попыток: S = S + 1; S = 0 + 1; S = 1.

13. S < 3, где 3 – контрольное число неудачных попыток для ручного счета.

14. Формируем новый случайный вектор :

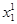= 0 + 0,36 · 4 =1,44

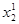= 1 + 0,91 · 5 = 5,55

(1,44; 5,55) Ï w Испытание неудачное.

12. Ведем счет неудавшихся попыток: S = S + 1; S = 1 + 1; S = 2.

13. S < 3, где 3 – контрольное число неудачных попыток для ручного счета.

14. Формируем новый случайный вектор :

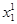= 0 + 0,25 · 4 =1,0

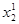= 1 + 0,31 · 5 = 2,55

(1,0;2,55) Îw

15. Вычисляем функцию штрафов в точке :

wZ() = 9· 1² + 9(2,55)² + 12·1,0 - 6·2,55+0,01 · (1,0 – 4)² +0,01 · (2,55 – 5)² +0,01 · (1 - 2,55)² = 64,39655.

11. Сравниваем wZ() и :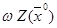

64,39655 > 3,32. Испытание неудачное.

12. Ведем счет неудавшихся попыток: S = S + 1; S = 2 + 1; S = 3.

13. S = 3, где 3 – контрольное число неудачных попыток для ручного счета. Процесс решения прекращаем.

Оптимальным решением является Х* = 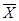⁰(0;1), WZ( 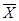⁰) =3,32;

min Z = Z ( 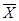^*)= Z(0,1)=12-6=3

Замечание. При решении на компьютере контрольное число неудавшихся попыток следует взять большим, например, 1000.