Различные алгоритмы градиентного метода (для самостоятельного изучения)

В любых алгоритмах используется движение по направлению вектора градиента, но алгоритмы отличаются по способу движения по направлению градиента.

1. Движение осуществляется до критической точки (как это осуществлялось в алгоритме наискорейшего подъёма или наискорейшего спуска). В этом случае определяется величина t*, которая задаёт глубину продвижения.

2. Движение осуществляется на заданный шаг ∆t, после чего снова определяется градиент z(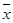 ₀ ) (градиентный метод движения шагами).

В этом случае координаты новой точки 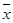определяем из условия:

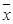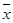= ₀ + ∆t ∙ 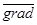z 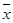₀ , или

х₁ = х₁⁰ + ∆t∙ 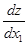( 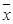₀ );

х₂ = х₂⁰ + ∆t∙ 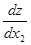( 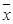₀ );

…

х_n = х_n⁰ + ∆t∙ 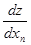( 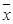₀ ); где ∆t – заданная величина.

3. Если для выбора направления движения используются несколько 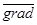z, вычисленных на предыдущих шагах, то такой метод получил название метода сопряжённых градиентов. В этом случае учитываются граничные значения нескольких 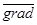z; новое значение градиента определяется как их линейная комбинация.