При слабой насыщенности сердечника, когда ВАХ катушки близка к прямой линии, т.е. доля высших гармоник в кривой тока мала, для анализа цепи применяется метод эквивалентных синусоид. Замена реальной кривой тока эквивалентной синусоидой позволяет пользоваться символическим методом расчета и строить векторные диаграммы.
При изменении основного магнитного потока 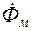 в сердечнике катушки по синусоидальному закону уравнение электрического состояния имеет вид
в сердечнике катушки по синусоидальному закону уравнение электрического состояния имеет вид
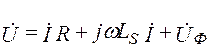 , (2.1)
, (2.1)
где 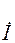 и
и 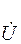 – соответственно ток и напряжение на катушке;
– соответственно ток и напряжение на катушке; 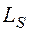 – индуктивность рассеяния, обусловленная потоком рассеяния;
– индуктивность рассеяния, обусловленная потоком рассеяния; 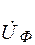 – напряжение, уравновешивающее ЭДС, наводимую основным магнитным потоком;
– напряжение, уравновешивающее ЭДС, наводимую основным магнитным потоком; 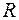 – активное сопротивление обмотки катушки.
– активное сопротивление обмотки катушки.
Схема замещения катушки приведена на рис. 2.1.
Напряжение 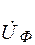 , называемое напряжением, соответствующим трансформаторной ЭДС, определяется по формуле
, называемое напряжением, соответствующим трансформаторной ЭДС, определяется по формуле

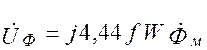 , (2.2)
, (2.2)
где 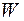 – число витков обмотки.
– число витков обмотки.
Можно допустить, что 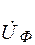 падает на участке схемы с сопротивлением
падает на участке схемы с сопротивлением 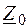 , которое можно разложить на составляющие по двум схемам, изображенным на рис. 2.1, с
, которое можно разложить на составляющие по двум схемам, изображенным на рис. 2.1, с 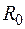 и
и 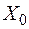 либо с
либо с 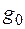 и
и 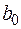 .
.
Таким образом, каждый из элементов 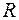 ,
, 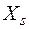 ,
, 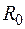 ,
, 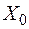 учитывает отдельные явления – потерю мощности в обмотке (меди)
учитывает отдельные явления – потерю мощности в обмотке (меди) 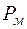 , рассеивание магнитного потока, потерю мощности в сердечнике (стали)
, рассеивание магнитного потока, потерю мощности в сердечнике (стали) 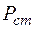 и прохождение в магнитопроводе основного магнитного потока, соответственно.
и прохождение в магнитопроводе основного магнитного потока, соответственно.
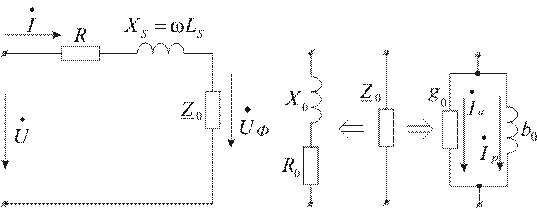
Рис. 2.1
Потери мощности в стали 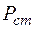 пропорциональны мощности петли гистерезиса материала сердечника, с другой стороны их можно определить по формуле
пропорциональны мощности петли гистерезиса материала сердечника, с другой стороны их можно определить по формуле
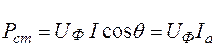 , (2.3)
, (2.3)
где 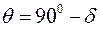 ;
; 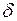 – угол магнитного запаздывания (потерь).
– угол магнитного запаздывания (потерь).
На рис. 2.2 показана векторная диаграмма катушки с ферромагнитным сердечником.
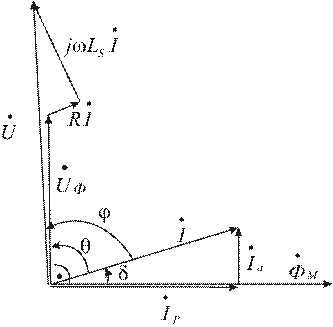
Рис. 2.2
 2015-07-04
2015-07-04 278
278








