Нелинейный метод наименьших квадратов

Задача заключается в обработке данных по формуле, которая нелинейно зависит от определяемых параметров. Пусть, например, предлагается описать экспериментальную зависимость некоторой величины y от x в виде гауссовой функции:

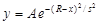(1)

где A, R и s – параметры, которые необходимо определить из условия, чтобы сумма квадратов отклонений величин, рассчитанных по этой формуле, от заданных (экспериментальных) значений была минимальной.

Рассмотрим задачу в общем случае, когда зависимость y от x требуется представить в виде

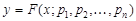(2)

где p₁, p₂,..., p_n – параметры, которые нужно определить так, чтобы эта формула наилучшим образом описывала имеющиеся данные — значения величины y в точках x₁, x₂, ¼, x_m, обозначаемые, соответственно, как y₁, y₂, ¼, y _m. Предполагается, что количество заданных точек m превышает число определяемых параметров n.

Запишем сумму квадратов отклонений функции F от значений y в заданных точках:

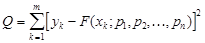(3)

Условием минимума этой суммы относительно параметров является равенство нулю частных производных:

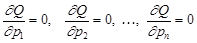(4)

Дифференцируя (3), получим уравнения:

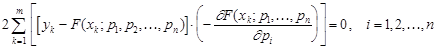. (5)

Систему уравнений (5) можно более компактно записать в матричной форме:

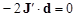
или, разделив на -2,

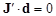(6)

где J – прямоугольная (m×n) матрица Якоби с элементами

,

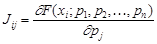знак ¢ обозначает транспонирование, а d – вектор-столбец размером m, составленный из отклонений в разных точках:

.

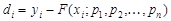Как матрица Якоби, так и элементы вектора d зависят от искомых параметров p₁,¼,p_n, причем эти параметры входят в функцию произвольного вида F, то есть (6), вообще говоря, представляет собой систему n нелинейных уравнений.

Попробуем построить метод численного решения системы (6), применяя те же идеи, что и в методе Ньютона. Предположим, что имеется начальное приближение 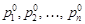для искомых параметров. Разложим элементы вектора d в ряд Тейлора в окрестности начального приближения и оставим в этом разложении только линейные члены. Результат можно записать в матричной форме следующим образом:

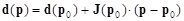(7)

(проверьте, что это действительно так). Здесь p обозначает совокупность n параметров p₁,¼,p_n; мы можем рассматривать p как n-мерный вектор. p₀ – вектор, соответствующий начальному приближению. Запись d(p) означает, что элементы вектора d вычислены при значениях параметров, представленных вектором p, а J(p₀) – матрица Якоби, вычисленная при начальном приближении p₀.

Подставляя (7) в уравнение (6), получим:

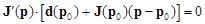. (8)

Обратите внимание, что в уравнении (6) фигурирует матрица Якоби, вычисленная в точке минимума, то есть J(p) и J(p₀), вообще говоря, различаются. Если бы не это обстоятельство, из (8) можно было бы найти вектор поправок Dp=p-p₀ к начальному приближению.

Заметим, что уравнение (8), в отличие от (6), не является точным, поскольку в нем использовано приближенное соотношение (7), полученное путем отбрасывания членов высших порядков в формуле Тейлора. Вероятно, степень точности уравнения (8) не ухудшится от введения еще одного приближения, если только дополнительная погрешность имеет величину того же порядка, что и погрешность (7). Исходя из этих соображений, будем считать, что J(p) и J(p₀) совпадают. Можно показать, что вносимая при этом в уравнение (8) ошибка соответствует членам второго и более высоких порядков относительно разности p-p₀, то есть такое приближение действительно находится на уровне точности уравнения (7). (Попробуйте доказать это утверждение самостоятельно).

Таким образом, из уравнения (8) окончательно получаем:

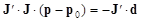, (9)

где матрица Якоби J и вектор отклонений d вычисляются в точке начального приближения, то есть при значениях параметров p₀. Мы получили систему линейных алгебраических уравнений для нахождения поправки Dp=p-p₀ к начальному приближению p₀. Обратите внимание, что система уравнений (9) очень похожа на систему нормальных уравнений линейного метода наименьших квадратов. Нетрудно убедиться, что в случае линейной зависимости функции F от параметров уравнение (7) становится точным, а матрица Якоби не зависит от p, так что (9) действительно превращается в точное уравнение линейного МНК.

В нелинейном случае уравнение (9) позволяет найти искомые параметры путем последовательных приближений. Так, задав начальное приближение p₀ и решив систему n уравнений с n неизвестными

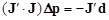
получим в качестве решения вектор поправок Dp, который следует добавить к начальному приближению:

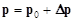
Найденные таким способом значения параметров p не являются точными в силу приближенного характера уравнения (9), но мы можем использовать их в качестве нового исходного приближения. Вновь решив систему (9), найдем новые поправки, добавим их к параметрам и т. д., пока поправки не станут достаточно малыми. Из (6) видно, что при достижении минимума суммы квадратов отклонений правые части уравнений (9), а следовательно и поправки, должны обратиться в нуль.

Описанный выше способ решения задачи нелинейного МНК носит название метода Гаусса-Ньютона. Как и метод Ньютона для нелинейных уравнений, он обладает квадратичной сходимостью. В частности, при обработке данных по формуле (1) параметры обычно перестают изменяться уже через 4-6 шагов, если было взято не слишком плохое начальное приближение.