1. Свойство коммутативности. Им обладают операции дизъюнкции, конъюнкции, эквивалентности, сложения по модулю 2, штрих Шеффера, стрелка Пирса
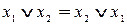 ;
; 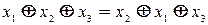 .
.
2. Свойство ассоциативности. Им обладают операции дизъюнкции, конъюнкции, эквивалентности, сложения по модулю 2.
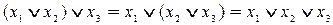 .
.
Функция импликации не имеет свойств коммутативности и ассоциативности, а функции Шеффера и Пирса не обладают свойством ассоциативности.
3. Свойство дистрибутивности. Им обладает конъюнкция относительно дизъюнкции и сложения по модулю 2, а также дизъюнкция относительно конъюнкции.
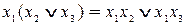
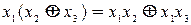
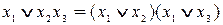
Если один из аргументов есть константа 1 или 0, то для элементарных функций получаем
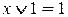
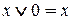
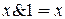
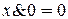
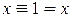
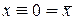
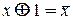
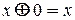 (11)
(11)
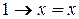
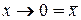
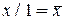
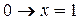
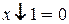
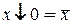
В том случае, когда 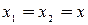 или
или 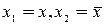 , получаем
, получаем
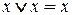
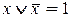
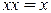
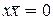
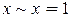
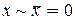 (12)
(12)
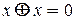
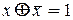
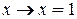
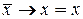
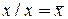
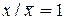 (13)
(13)
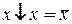
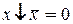 (14)
(14)
 2015-07-21
2015-07-21 278
278








