Некоторые функции от n =0,1,2 аргументов называются элементарными и для них введены специальные обозначения.
При n=0 имеются 2 различные функции
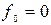 ,
, 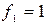 .
.
При n=1 получим 4 функции
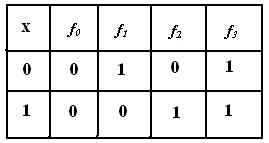
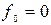 ,
, 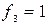 уже известны,
уже известны, 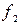 =
= 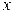
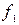 =
= 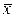 .
.
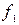 называется отрицанием x или инверсией x.
называется отрицанием x или инверсией x.
Пусть n=2, получаем 16 функций.
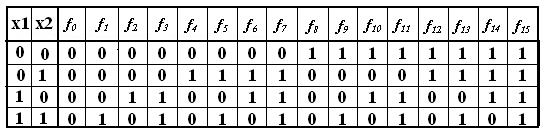
Функции 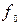
 =0,
=0, 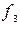 =
= 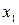 ,
, 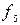 =
= 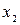 ,
, 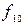 =
= 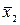 ,
, 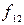 =
= 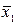 ,
, 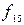 =1 уже встречались при n=0,1. Функции
=1 уже встречались при n=0,1. Функции 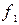 ,
, 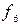
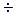
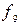 ,
, 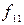 ,
, 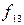 ,
, 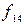 считаются элементарными и для них введены специальные обозначения.
считаются элементарными и для них введены специальные обозначения.
Функция 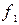 называется конъюнкцией (логическим умножением), обозначается символом & или
называется конъюнкцией (логическим умножением), обозначается символом & или 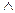 , который часто опускается
, который часто опускается
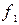 =
= 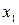
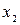 .
.
Функции 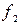 =
= 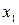
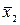 и
и 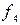 =
= 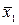
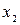 не считаются элементарными.
не считаются элементарными.
Функция 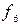 называется сложением по модулю 2.
называется сложением по модулю 2.
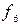 =
= 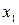
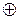
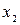 .
.
Функция 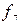 называется дизъюнкцией (логическим сложением)
называется дизъюнкцией (логическим сложением)
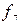 =
= 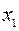
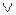
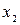 .
.
Функция 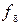 называется функцией Вебба (стрелка Пирса)
называется функцией Вебба (стрелка Пирса)
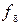 =
= 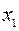
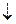
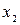 .
.
Функция 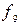 называется функцией эквивалентности
называется функцией эквивалентности
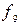 =
= 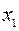 ~
~ 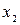 =
= 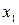
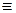
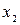 .
.
Функции 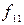 (
(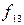 ) называются импликациями (вхождениями) и обозначаются
) называются импликациями (вхождениями) и обозначаются
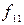 =
= 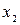
 ,
, 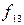 =
= 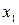
 .
.
Функция 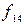 называется штрихом Шеффера
называется штрихом Шеффера
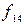 =
= 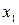 /
/ 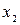 .
.
 2015-07-21
2015-07-21 324
324








