2015-07-21
426
Используя выражения (15) и (16), любую функцию можно записать в виде СДНФ или СКНФ. Но эти формы далеки от минимальных..
Пример 9. Пусть задана СДНФ функции
.
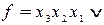
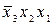
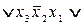
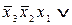
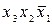Функция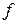 
в базисе (21) имеет вес 
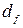=14. Преобразуем функцию 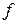. Добавим еще один дизъюнктивный член 
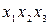. Это добавление не меняет 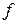, т.к..
,
= 
.
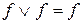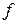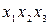
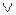
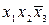
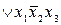
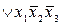
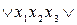
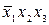Используем свойства ассоциативности и дистрибутивности
= 
.
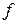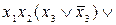
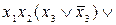
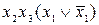Учитывая, что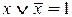 
, 
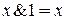. Получим = 
,
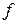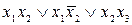преобразуем =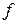 
,
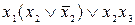получим =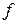 
.
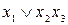н
Все методы минимизации основаны на применении к функции, заданной в виде СДНФ двух операций:
1. Операция неполного склеивания
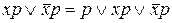. (22)
2. Операция поглощения
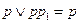. (23)
Последовательно применяя эти операции можно построить минимальную ДНФ функции.
Наиболее распространенным методом нахождения минимальной ДНФ функции является метод карт Карно (диаграмма Вейча).
