Основная цель измерений – количественная оценка значения физической величины в принятых для нее единицах. Информацию об этой физической величине и ее значении несет сигнал измерительной информации.
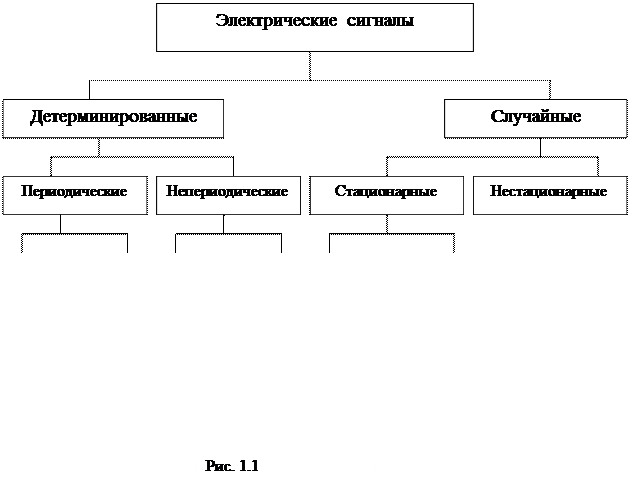
По характеру изменения во времени все сигналы можно классифицировать как детерминированные и случайные (недетерминированные). Классификация электрических сигналов представлена на схеме рис.1.1.
Мы с вами рассмотрим только детерминированные сигналы, так как, в основном, будем иметь дело с ними.
К детерминированным относятся сигналы, описываемые математическими соотношениями, мгновенные значения которых в любой момент времени известны, например, синусоидальный сигнал.
Детерминированные сигналы могут быть периодическими или непериодическими. Периодические сигналы делятся на синусоидальные (гармонические) и несинусоидальные (полигармонические). К непериодическим сигналам относятся почти периодические и переходные.
Синусоидальный (гармонический) сигнал можно описать функцией времени t:
u(t)=Um sin (2pft + y),
где u(t) – мгновенное значение напряжения, В; Um – амплитуда напряжения, В; f=1/T – частота (число полных периодов Т, измеряемое в единицу времени), Гц; y- начальная фаза, рад.
Синусоидальный сигнал является частным случаем несинусоидального. Несинусоидальный сигнал можно представить рядом Фурье:
u(t)=U 0 + 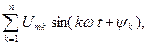
где U 0 – среднее значение сигнала за период Т (постоянная составляющая); Umk – амплитуда сигнала k- ой гармоники.
       |
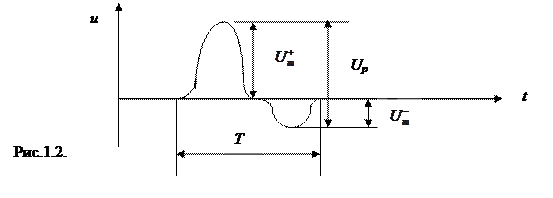
На рис.1.2 представлен несинусоидальный разнополярный периодический сигнал – напряжение (ток), характеристиками которого являются: u(t) – значение сигнала в заданный момент времени; 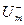 и
и 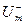 - пиковые значения сигнала – наибольшее мгновенное значение положительной полуволны и наименьшее мгновенное значение отрицательной полуволны сигнала (Um – амплитудное значение для синусоидального сигнала); Up (размах) – сумма модулей пиковых значений
- пиковые значения сигнала – наибольшее мгновенное значение положительной полуволны и наименьшее мгновенное значение отрицательной полуволны сигнала (Um – амплитудное значение для синусоидального сигнала); Up (размах) – сумма модулей пиковых значений 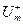 и
и 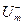 .
.
 |
Постоянная составляющая сигнала – среднее значение сигнала за период Т
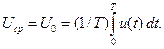
Переменная составляющая сигнала за период – разность между мгновенным значением сигнала и его постоянной составляющей:
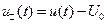 .
.
Средневыпрямленным значением сигнала за период является среднее значение модуля сигнала:
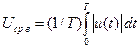
(вводится для сигналов, симметричных относительно оси времени).
Среднеквадратическое значение сигнала за период (время измерения)
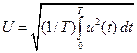 .
.
Для синусоидального сигнала среднеквадратическое значение называют действующим значением сигнала.
Основная характеристика сложных сигналов – их спектральная функция, дающая информацию об амплитудах и фазах отдельных гармоник.
Среднеквадратическое значение периодического несинусоидального сигнала
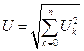 ,
,
где 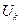 - среднеквадратическое значение k- ой гармоники; k – номер гармоники.
- среднеквадратическое значение k- ой гармоники; k – номер гармоники.
Коэффициенты амплитуды и формы устанавливают связь между указанными выше значениями сигнала:
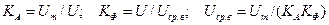 .
.
Для синусоидального сигнала
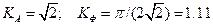 .
.
Детерминированные сигналы конечной энергии, существенно отличные от нуля в течение ограниченного интервала времени называются импульсными сигналами. Импульсы бывают различной формы (прямоугольной, треугольной, трапецеидальной и др.), полярности, амплитуды, длительности, частоты следования. Наиболее часто в практике встречаются прямоугольные импульсы (рис.1.3), у которых среднеквадратическое значение и постоянная составляющая вычисляются как
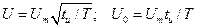 .
.
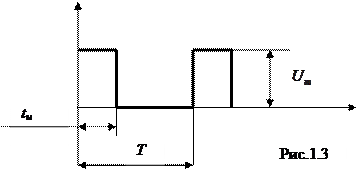 |
Периодическая последовательность прямоугольных импульсов с амплитудой Um, длительностью tu, периодом повторения Т характеризуется скважностью Q=T/tu. При этом 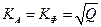 . Следовательно, среднеквадратическое значение
. Следовательно, среднеквадратическое значение 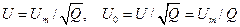 .
.
Для некоторых, часто используемых, форм сигнала коэффициенты амплитуды и формы вычислены. Например, для треугольной формы (рис.1.4) 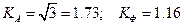 . Для меандра (рис.1.5) -
. Для меандра (рис.1.5) - 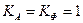 .
.
 |
 2015-07-21
2015-07-21 1682
1682







