Лабораторная работа
ИССЛЕДОВАНИЕ РЕЗОНАНСНЫХ СВОЙСТВ
КОЛЕБАТЕЛЬНОГО КОНТУРА
Цель работы
Целью данной работы является экспериментальное определение резонансной частоты, полосы пропускания и добротности контура, а также сравнение экспериментальных результатов с соответствующими теоретическими значениями.
Приборы и принадлежности
1 Звуковой генератор ГЗ -33
2 Катушка индуктивности
3 Набор конденсаторов
4 Магазин сопротивлений
5 Вольтметр
6 Соединительные провода
Введение
Рассмотрим колебательный контур (рисунок 1), состоящий из последовательно соединенных емкости С, индуктивности L и резистора R. Контур подключен к источнику ЭДС 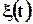 , которая меняется во времени по гармоническому закону с частотой
, которая меняется во времени по гармоническому закону с частотой 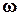 :
: 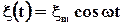
 |

Рисунок 1
Для анализа процессов в контуре применим закон Ома к участку цепи 1-а-2. С учетом ЭДС самоиндукции 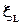 в индуктивности имеем:
в индуктивности имеем:
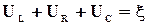 , (1)
, (1)
Решая это уравнение, получим закон Ома для цепи переменного тока:
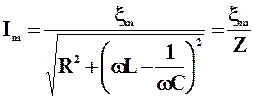 , (2)
, (2)
где величина 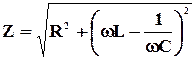 называется полным сопротивлением колебательного контура: (импедансом),
называется полным сопротивлением колебательного контура: (импедансом), 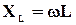 – индуктивным сопротивлением, а
– индуктивным сопротивлением, а 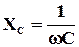 – емкостным сопротивлением.
– емкостным сопротивлением.
Как видно из (2), амплитуда тока в контуре зависит от частоты 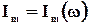 . Эта зависимость называется амплитудно-частотной характеристикой контура (АЧХ). При условии
. Эта зависимость называется амплитудно-частотной характеристикой контура (АЧХ). При условии 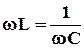 полное сопротивление контура минимально
полное сопротивление контура минимально 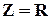 , а амплитуда тока в контуре будет максимальна. Говорят, что имеет место резонанс. Резонансная частота (частота, при которой достигается максимум тока), определяется из этого условия и равна
, а амплитуда тока в контуре будет максимальна. Говорят, что имеет место резонанс. Резонансная частота (частота, при которой достигается максимум тока), определяется из этого условия и равна
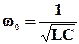 . (3)
. (3)
Видно, что резонансная частота для тока совпадает с частотой собственных колебаний в контуре. Таким образом, резонансом называется явление резкого возрастания амплитуды при приближении частоты вынужденных колебаний к частоте собственных колебаний системы.
При отклонении частоты генератора от резонансной частоты амплитуда тока уменьшается и обращается в нуль как при ω = 0, так и при ω → ∞. На рисунке 2 показана амплитудно-частотная характеристика 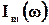 , называемая резонансной кривой.
, называемая резонансной кривой.
Остроту резонанса принято оценивать шириной резонансной кривой 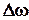 на уровне
на уровне 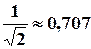 от максимального значения амплитуды тока в резонансе. Безразмерная величина, равная отношению резонансной частоты к полосе пропускания, называется добротностью контура
от максимального значения амплитуды тока в резонансе. Безразмерная величина, равная отношению резонансной частоты к полосе пропускания, называется добротностью контура
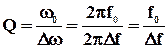 (4)
(4)
Чем острее резонансная кривая, тем больше добротность контура.
Найдем связь между добротностью 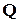 и параметрами контура R, L и C. Значение частот, при которых амплитуда тока
и параметрами контура R, L и C. Значение частот, при которых амплитуда тока 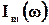 составляет 0,707 от максимального значения амплитуды в резонансе
составляет 0,707 от максимального значения амплитуды в резонансе 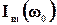 , можно найти из соотношения (2). Должно выполняться условие
, можно найти из соотношения (2). Должно выполняться условие
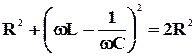 .
.
Отсюда
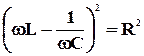
Это биквадратное уравнение можно разделить на два квадратных уравнения
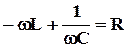 и
и 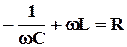 .
.
Положительные корни этих уравнений равны:
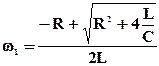 и
и 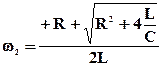 .
.
Тогда ширина резонансной кривой равна:
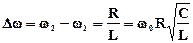 , (5)
, (5)
отсюда добротность
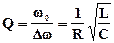 . (6)
. (6)
Соотношение (6) показывает, что чем меньше активное сопротивление контура R, тем больше его добротность и, следовательно, тем острее резонансная кривая.
 |
Рисунок 2
Добротность контура можно выразить через логарифмический декремент затухания колебательного контура 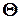 . Поскольку
. Поскольку 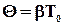 где
где 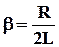 – коэффициент затухания, а
– коэффициент затухания, а 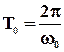 – период собственных колебаний, то подставляя эти значения, получаем
– период собственных колебаний, то подставляя эти значения, получаем 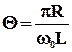 . Используя, согласно (6), соотношение
. Используя, согласно (6), соотношение 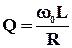 , находим:
, находим: 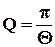 .
.
 2015-07-21
2015-07-21 443
443







