Сущность и основные свойства преобразования Лапласа

Изображение Л - 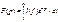f(p)-функция интеграла p-комплексная переменная;

F(p)=Z{f(t)}

Основные свойства

1 Линейность, т.е. линейность комплектации оригинала соотв. такая же лин. комбинация

изображения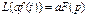

2 n-кратному дифф. Оригинала соответствует (степень) умножения на p в степени n

3 интегралу соответ. деление на рлп.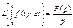

4 Теорема запаздывания смещение аргумента оригинала на величину a соотв. умножения оригинала на величину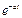

5 смещение аргумента изображения на величину a соотв. умножения функции на величину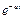

6 Теорема масштабов умножение аргумента оригинала на постоянную величину a соотв. делению изображения и его аргумента на величину a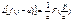

Вывод применение изображения Л позволяет заменить операции диффер. и интегрирования на обычные алгебраические позиции.