2015-07-21
362
При оценке организации расчетно-кассового обслуживания юридических лиц в отделениях банка было проведено выборочное обследование, в ходе которого оценивался показатель Х – списания наличных денежных средств со счетов юридических лиц (в %):
| январь | февраль | март | апрель | май | июнь | июль | август | сентябрь | октябрь | ноябрь | декабрь | |
| 2011г. |
1. Выполнить первичную статистическую обработку данных группировку за 2011 год, представив их в форме дискретного вариационного ряда и рассчитать выборочные статистические характеристики, пояснив смысл полученных результатов
2. Полагая, что изменчивость показателя Х можно описать законом нормального распределения, построить γ-ый доверительный интервал (γ=0,9) для ожидаемого среднего значения изучаемого показателя Х.
3. Проверить статистическую гипотезу о том, среднее значение признака X будет равно 20, на уровне значимости 10%.
РЕШЕНИЕ:
1 шаг. Составим исходную расчетную таблицу (см.таблицу 1), записывая в нее данные только за один указанный год. Находим суммы по строкам таблицы:
|
|
|
Таблица 1.
| январь | февраль | март | апрель | май | июнь | июль | август | сентябрь | октябрь | ноябрь | декабрь | суммы | |
| Х | |||||||||||||
| Х2 |
2 шаг. Рассчитаем выборочные статистические характеристики признака Х для дискретного вариационного ряда малого объема выборки, используя формулы (1.1):
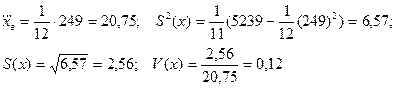
Смысл полученных результатов состоит в следующем:
Величина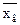 
- характеризует среднее значение показателя Х в пределах рассматриваемой выборки, поэтому средний процент списания наличных денежных средств со счетов юридических лиц составил 20,75 %.
«Исправленное» стандартное отклонение описывает абсолютный разброс значений показателя Х и в данном случае составляет 2,56%.
Коэффициент вариации характеризует относительную изменчивость показателя Х вокруг среднего значения и в данном случае равен 0,12%.
3 шаг. Полагая, что изменчивость показателя X можно описать законом нормального распределения, построим доверительный интервал для ожидаемого среднего значения признака Х исходя из неравенства (1.2), где предельную ошибку выборки рассчитываем по формуле (1.3), где значение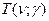 
- коэффициента доверия, зависящего от числа степеней свободы 
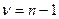и заданного значения доверительной вероятности находим по таблице ПРИЛОЖЕНИЯ 1.: 
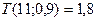, тогда предельная ошибка равна:
,
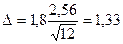в результате доверительный интервал определяется неравенством:
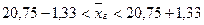или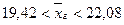 
Вывод: смысл полученных результатов состоит в том, что на основании результатов выборочного обследования с надежностью 0,9 можно утверждать, что средняя норма списания наличных средств со счетов юридических лиц находится в пределах от 19,42% до 22,08%.
|
|
|
4 шаг. Для проверки статистической гипотезы о числовом значении параметра X используем критерий Стьюденса.
Выдвигаем 2 гипотезы:
Н0: М(X)=20 и Н1: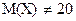 
Выбираем подходящий критерий проверки для Н0. В качестве критерия можно рассматривать: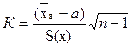 
= 
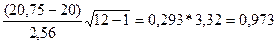
Исходя из условий задачи, задаемся уровнем значимости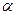 
=0,1 и находим по специальным таблицам ккр. В данном случае используем таблицы Стьюдента (коэффициента доверия), зависящего от числа степеней свободы 
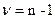и уровня значимости : 
= .
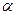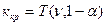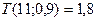Выясняем, в какую область попадает значение К. Если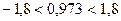 
, то гипотеза Н0 принимается.
