Вычислим 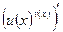 . Для этого вычислим двумя способами
. Для этого вычислим двумя способами 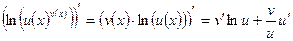
и
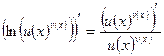 .
.
Таким образом, получим важную формулу
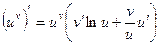 .
.
Пример 1. Вычислим 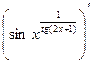 .
.
Здесь 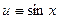 ,
, 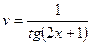 . Отсюда
. Отсюда 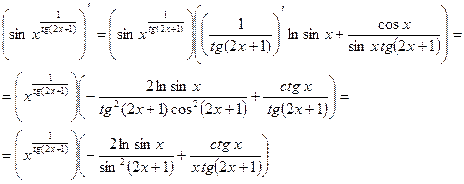
Пример 2. 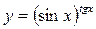
Решение. Имеем 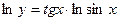 , откуда
, откуда 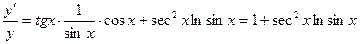 ;
; 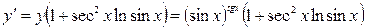
Пример 3. 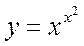
Решение Здесь основание и показатель степени зависят от 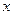 . Логарифмируя, получим
. Логарифмируя, получим 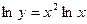 . Продифференцируем обе части последнего равенства по
. Продифференцируем обе части последнего равенства по 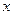 . Так как
. Так как 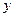 является функцией от
является функцией от 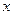 , то
, то 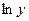 есть сложная функция
есть сложная функция 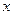 и
и 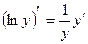 . Следовательно,
. Следовательно, 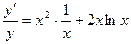 ,
, 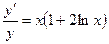 , т.е.
, т.е. 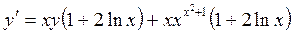
Производная параметрической функции
Если функция задана параметрическими уравнениями 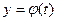 ,
, 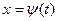 , то
, то
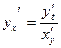 или
или 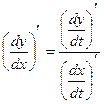 .
.
Пример 1. Вычислите производную 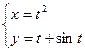
Решение. 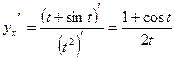 .
.
Пример 2. Найти 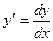 , если
, если 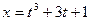 ,
, 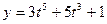
Решение. Найдём 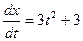 ,
, 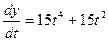 . Следовательно
. Следовательно 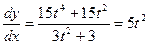
Приложения производной к задачам геометрии и механики.
Если кривая задана уравнением 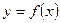 , то
, то 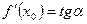 , где
, где 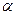 - угол, образованный с положительным направлением оси
- угол, образованный с положительным направлением оси 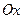 касательно к кривой в точке с абсциссой
касательно к кривой в точке с абсциссой 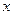 .Уравнение касательной к кривой
.Уравнение касательной к кривой 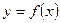 в точке
в точке 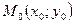 имеет вид
имеет вид
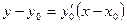
где 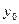 есть значение производной
есть значение производной 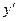 при
при 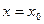 . Нормалью к кривой называется прямая, перпендикулярная касательной, проходящая через точку касания. Уравнение нормали имеет вид:
. Нормалью к кривой называется прямая, перпендикулярная касательной, проходящая через точку касания. Уравнение нормали имеет вид:
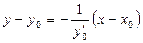
Углом между двумя кривыми 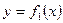 и
и 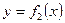 в точке их пересечения
в точке их пересечения 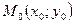 называется угол между касательными к этим кривым в точке
называется угол между касательными к этим кривым в точке 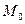 . Этот угол находиться по формуле:
. Этот угол находиться по формуле:
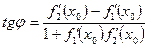
Если при прямолинейном движении точки задан закон движения 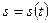 , то скорость движения в момент
, то скорость движения в момент 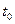 есть производная пути во времени:
есть производная пути во времени: 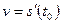
Пример 1. Какой угол образует с осью абсцисс касательная к кривой 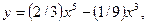 проведённая в точке
проведённая в точке 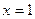 ?
?
Решение. Находим производную 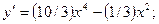 при
при 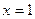 имеем
имеем 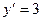 т.е.
т.е. 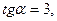 откуда
откуда 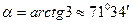 .
.
 2015-07-14
2015-07-14 515
515







