Определение производной
Пусть 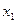 и
и 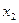 -два значения аргумента
-два значения аргумента 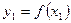 и
и 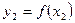 соответствующие значения функции
соответствующие значения функции 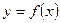 . Разность
. Разность 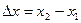 называется приращением аргумента. Разность
называется приращением аргумента. Разность 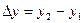 называется приращением функции на отрезке
называется приращением функции на отрезке 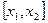 .
.
Определение. Производной от функции 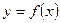 называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю.
называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю.
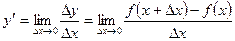 .
.
Геометрически, производная представляет собой угловой коэффициент касательной к графику функции 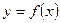 . Производная есть скорость изменения функции
. Производная есть скорость изменения функции 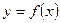
Таблица производных
1) 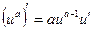 ,
, 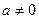 ;
;
2) 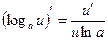 , при
, при 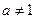 ;
;
3) 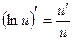 ;
;
4) 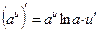 ,
, 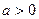 ;
; 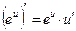 ;
;
5) 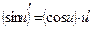 ;
;
6) 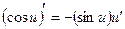 ;
;
7) 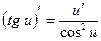 ;
;
8) 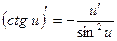 ;
;
9) 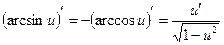 ;
;
10) 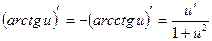 .
.
Правила дифференцирования функций
Пусть С- постоянная и 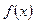 ,
, 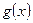 - дифференцируемые функции. Тогда:
- дифференцируемые функции. Тогда:
1) 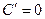
2) 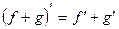
3) 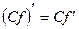
4) 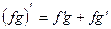
5) 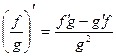 ,
, 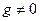
6) Производная сложной функции, т.е. функции, зависящей от некоторой другой функции, 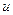 , вычисляется при помощи таблицы производных.
, вычисляется при помощи таблицы производных. 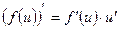 , где
, где 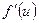 находится с использованием таблицы.
находится с использованием таблицы.
 2015-07-14
2015-07-14 204
204







