2015-07-21
2409
В связи с тем, что ЭПР объекта существенно зависит от его формы и линейных размеров по сравнению с длиной облучающей волны λ, выбором малоотражающей формы объекта можно добиться значительного снижения его ЭПР.
С точки зрения формы наименьшей ЭПР обладает конус при его облучении со стороны вершины. При отклонении направления облучения плоского листа от нормали к поверхности цели плоская поверхность также имеет низкое значение ЭПР. Поэтому для радиомаскировки объектов с высокой эффективностью используют наклонные экранирующие плоскости (радиолокационные экраны).
Плоские поверхности при облучении под прямым углом имеют значительную величину ЭПР. Поэтому с целью снижения радиолокационной заметности объектов плоские поверхности заменяют гофрированными, которые преобразуют зеркальное отражение радиоволн в диффузное рассеяние.
Так, например, только в результате совершенствования формы американские фирмы снизили ЭПР стратегических бомбардировщиков со 100 м2 (В-52) до 1м2 (В-1В), а тактических истребителей с 5 м2 (F-4) до 1,7 м2 (F-16).
|
|
|
Контрольные вопросы.
Вопрос 1. РЛС с рабочей длиной волны λ = 10 см облучает плоскую квадратную пластину со стороной 1 м и уголковые отражатели с треугольными и квадратными гранями.
Определить:
а). ЭПР плоской квадратной пластины при облучении под прямым углом и под углом облучения Θ = 50;
б). ЭПР уголкового отражателя с треугольными и квадратными гранями при такой же длине ребра.
Сравнить их ЭПР и сделать выводы.
Решение:
а). ЭПР квадратной пластины при облучении под прямым углом:
σ = 
= 1256 м2.
ЭПР квадратной пластины при угле облучения Θ = 50:
σ =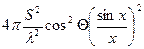 
,
где: x =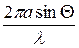 
; S = a2.
Отсюда:
x =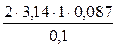 
≈ 5,47
σ =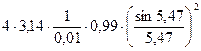 
≈ 21,8 м2.
б). ЭПР уголкового отражателя с треугольными гранями:
σ =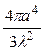 
= 
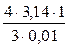≈ 419 м2.
ЭПР уголкового отражателя с квадратными гранями:
σ =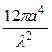 
= 
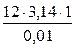≈ 3768 м2.
Выводы:
- ЭПР плоской квадратной пластины при облучении под прямым углом примерно в 3 раза больше, чем ЭПР уголкового отражателя с треугольными гранями.
Однако при отклонении направления облучения плоской пластины от нормали к поверхности даже на 50 ее ЭПР уменьшается почти в 100 раз. В то же время ЭПР обычного уголкового отражателя остается постоянной в пределах угла облучения порядка 450.
- ЭПР уголкового отражателя с квадратными гранями примерно в 9 раз больше, чем ЭПР уголкового отражателя с треугольными гранями.
Вопрос 2. РЛС работает в сантиметровом диапазоне волн с длиной волны, равной:
а). λ = 3 см;
б). λ = 10 см;
с). λ = 0,5 м2.
Определить:
Количество дипольных отражателей, необходимое для имитации стратегического бомбардировщика В-1 (σ =10 м2) и сделать вывод.
|
|
|
Решение:
Количество дипольных отражателей, которое необходимо для имитации ЭПР σ = 10 м2:
n = σ/σdo sr = σ/0,17λ2
а). n = 10/0,17·9·10-4 ≈ 65360 ≈ 65000 шт;
б). n ≈ 5882 ≈ 6000 шт;
с). n ≈ 235 шт.
Вывод:
Для имитации точечной цели на экране РЛС, работающей в метровом диапазоне волн достаточно иметь сотни дипольных отражателей. В сантиметровом диапазоне волн их количество возрастает до нескольких десятков тысяч. Однако с учетом эффекта слипания и излома отражателей для получения требуемого значения ЭПР фактическое количество дипольных отражателей должно быть в 2 – 3 раза больше.
Вопрос 3. РЛС с рабочей длиной волны λ = 10 см облучает плоскую квадратную пластину площадью S = 1м2, а также шар и конус с такой же площадью поперечного сечения. Падающая электромагнитная волна образует с плоскостью пластины прямой угол.
Определить:
а). ЭПР квадратной пластины при угле облучения Θ = 150;
б). ЭПР шара;
в). ЭПР конуса, если направление падающей волны совпадает с осью конуса, а угол при его вершине α = 600.
Сделать вывод относительно формы цели, обладающей наименьшей величиной ЭПР.
Решение:
а). ЭПР квадратной пластины:
σ = 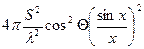≈ 1,2 м2,
где: x = 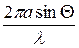≈ 16,25; S = 1м2.
б). ЭПР шара:
σ = πR2 = 1м2.
в). ЭПР конуса:
σ = πR2tg2α = 0,33 м2.
Выводы:
- С точки зрения формы цели наименьшей ЭПР обладает конус.
- Если направление облучения плоской пластины не совпадает с нормалью к ее поверхности, то ее ЭПР также резко снижается.
