Как можно отблагодарить автора?

Как построить график функции
с помощью геометрических преобразований графиков?

Долгое время мне не хватало решимости подойти к детальной разработке раздела о полном исследовании функции, поскольку тема весьма обширна и предполагает построение большого количества графиков. Но после аналитической геометрии не страшны уже и чертежи ядерной электростанции, поэтому без колебаний возьмём в свои руки острозаточенные карандаши и длинные линейки. Не беспокойтесь по поводу значительного размера веб страницы – здесь очень много чертежей и важнейшей прикладной информации, которая потребуется в будущем.

Чайникам и вновь прибывшим посетителям рекомендую, прежде всего, ознакомительную статью Графики и свойства элементарных функций, где мы рассмотрели основные методы и правила построения графиков. И следующая ступень посвящения – геометрические преобразования графиков функций.

Что это такое? Рассмотрим какую-нибудь элементарную функцию, например, 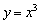. Подавляющему большинству читателей не составит труда построить кубическую параболу, но что делать, если требуется начертить график функци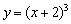и или 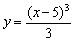? Интуиция подсказывает, что совершенно не нужно тратить уйму времени и проводить полное исследование функции, достаточно выполнить некоторые геометрические преобразования кубической параболы 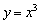. График функции можно сжимать/растягивать, сдвигать вдоль осей, симметрично отображать. То есть, несколько волшебных пассов, и кривые 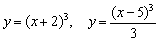готовы!

Зачем это нужно? Вы скажете, что можно применить метод поточечного построения, о котором я так много говорил в методичке о графиках функций. Вот взять ту же функцию 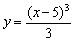и построить её по точкам! Да, способ рабочий. Однако знания геометрических преобразований позволят вам быстро понять, как расположен график, а в несложных случаях вроде 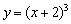практически мгновенно его нарисовать! Навыки грамотно разбираться с чертежами потребуются в различных задачах высшей математики, например, при исследовании функции на непрерывность, нахождении площади фигуры, объема тела вращения, в ходе вычисления двойных интегралов и т.д.

Кроме того, поточечное построение бывает не всегда удобным, так, значения периодической функции 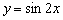можно находить до нервного смеха. Конечно, существуют специальные программы для построения графиков, онлайн сервисы, но они далеко не всегда бывают под рукой.

Иногда на практике задание встречается отдельно, примерная формулировка такова: «построить график функции, используя преобразования графиков элементарных функций». Дана, скажем, функция 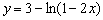. Задача состоит в том, чтобы с помощью геометрических преобразований ветки логарифма 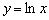получить график функции .

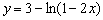Среди прочего материала мы рассмотрим функции с модулем, незаслуженно обойдённые вниманием на первом уроке. По существу, модуль тоже влечёт вполне определённое преобразование графика функции.

Перед тем как перейти непосредственно к примерам напомню некоторые теоретические моменты. В начале статьи о дифференцировании неявной функции я сформулировал определение функции одной переменной 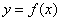. Актуализирую два особо нужных сейчас термина: «икс» – независимая переменная или АРГУМЕНТ, «игрек» – зависимая переменная или ФУНКЦИЯ. При этом функцию можно обозначать как через «игрек», так равноценно и через «эф от икс», например:

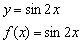
Данный технический момент уже упоминался на уроке Типовые задачи с производной. Разницы особой нет, но есть традиции, и в теме «Функции и графики» значительно чаще используется обозначение .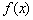

Арсенал преобразований графиков разнообразен как набор пыток святой инквизиции. Приступим =)

Сжатие (растяжение) графика к (от) оси ординат.
Симметричное отображение графика относительно оси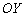

Первая группа действий связана с умножением АРГУМЕНТА функции на число. Для удобства я разобью правило на несколько пунктов: