Вертикальные асимптоты графика функции

Вертикальная асимптота графика, как правило, находится в точке бесконечного разрыва функции. Всё просто: если в точке 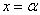функция 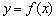терпит бесконечный разрыв, то прямая, заданная уравнением 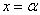является вертикальной асимптотой графика.

Примечание: обратите внимание, что запись 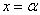используется для обозначения двух совершенно разных понятий. Точка подразумевается или уравнение прямой – зависит от контекста.

Таким образом, чтобы установить наличие вертикальной асимптоты 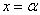в точке 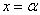достаточно показать, что хотя бы один из односторонних пределов 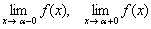бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции. Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова – любите и жалуйте вертикальную асимптоту. Простейшая иллюстрация: 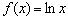и ось ординат (см. Графики и свойства элементарных функций).

Из вышесказанного также следует очевидный факт: если функция непрерывна на 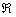, то вертикальные асимптоты отсутствуют. На ум почему-то пришла парабола. Действительно, где тут «воткнёшь» прямую? …да… понимаю… последователи дядюшки Фрейда забились в истерике =)

Обратное утверждение в общем случае неверно: так, функция 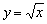не определена на всей числовой прямой, однако совершенно обделена асимптотами.