Точки разрыва функции – это точки 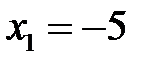 и
и 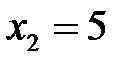 , в которых функция не определена. Вычислим пределы функции в этих точках:
, в которых функция не определена. Вычислим пределы функции в этих точках:
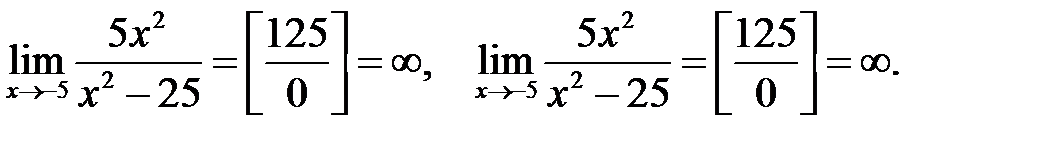
Поэтому прямые с уравнениями  и
и  являются вертикальными асимптотами графика функции.
являются вертикальными асимптотами графика функции.
Невертикальные асимптоты графика функции.
Невертикальной асимптотой будем называть асимптоту, не параллельную оси Оу. Невертикальная асимптота графика функции  при
при 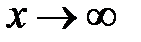 существует тогда и только тогда, когда существуют конечные пределы
существует тогда и только тогда, когда существуют конечные пределы
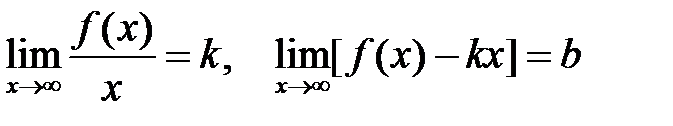 .
.
Эта асимптота имеет уравнение 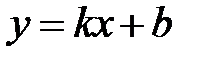 .
.
Вычислим пределы
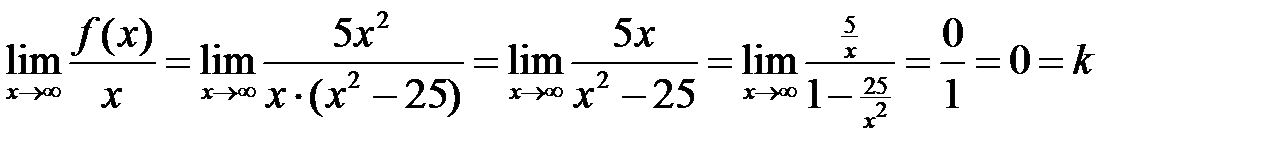 ,
,
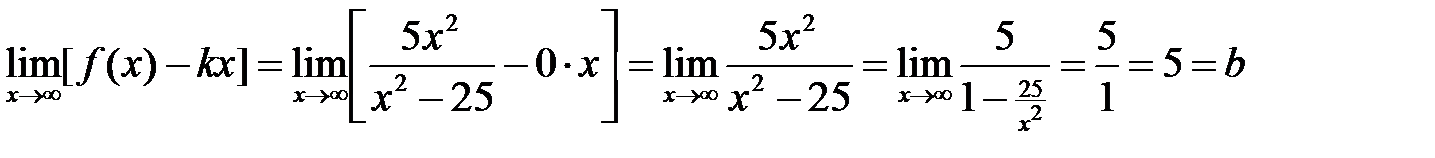 .
.
Так как оба предела 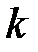 и
и 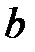 конечны, то график функции имеет невертикальную асимптоту при
конечны, то график функции имеет невертикальную асимптоту при 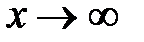 . Её уравнение
. Её уравнение 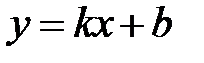 , то есть
, то есть 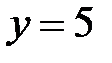 .
.
Построение графика функции.
На основании результатов проведенного исследования строим график функции.
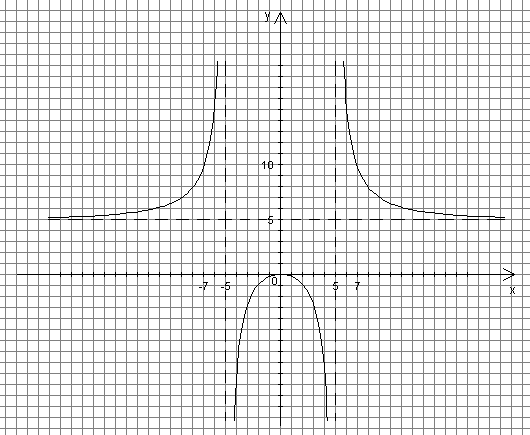
Рис. 1
Четность функции облегчает построение графика: строим часть графика функции для значений 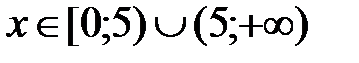 , а затем отображаем эту часть графика симметрично относительно оси ординат и получаем весь график.
, а затем отображаем эту часть графика симметрично относительно оси ординат и получаем весь график.
Для уточнения графика рассмотрим несколько дополнительных точек:
|
|
|
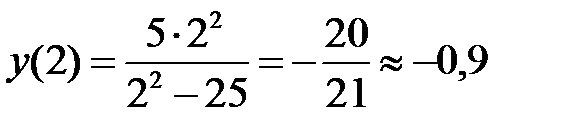 ,
, 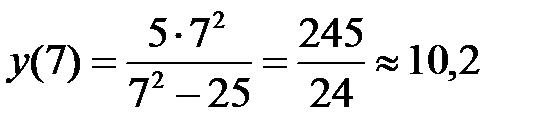 .
.
9. Множество значений функции.
Вид графика (см. рис. 3.1) позволяет сделать вывод, что 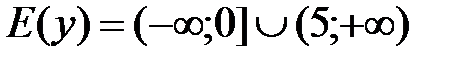 .
.
Индивидуальные задания
Исследовать методами дифференциального исчисления функцию 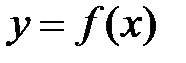 и на основании полученных результатов построить её график.
и на основании полученных результатов построить её график.
1. 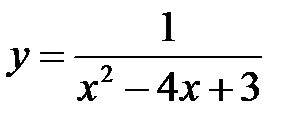 . 2.
. 2. 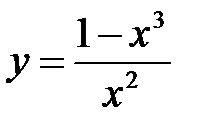 .
.
3. 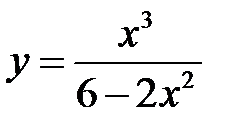 . 4.
. 4. 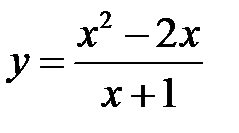 .
.
5. 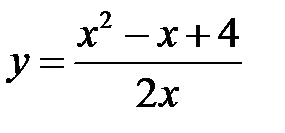 . 6.
. 6.  .
.
7. 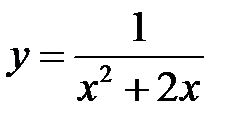 . 8.
. 8. 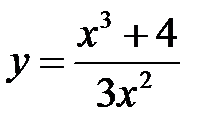 .
.
9. 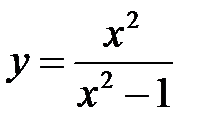 . 10.
. 10. 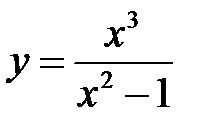 .
.
ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Практическая часть
Задание 1. Изобразить область определения 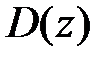 функции двух переменных
функции двух переменных  .
.
Функция  определена во всех точках, координаты
определена во всех точках, координаты 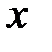 и
и 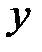 которых удовлетворяют неравенству
которых удовлетворяют неравенству  или
или 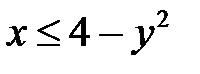 . Уравнение
. Уравнение 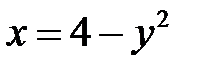 задаёт параболу, а неравенству
задаёт параболу, а неравенству 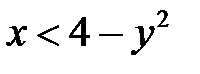 удовлетворяют координаты точек плоскости, расположенных левее этой параболы:
удовлетворяют координаты точек плоскости, расположенных левее этой параболы:
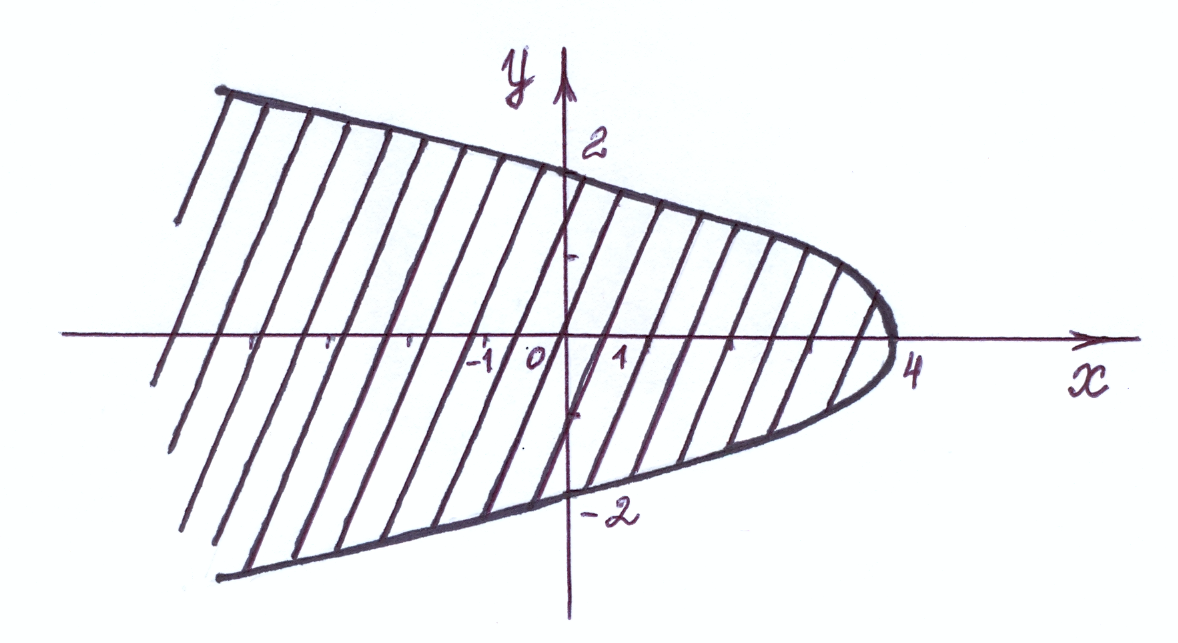
Рис.2.
Область определения 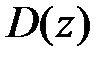 функции
функции  изображена на рис.4.
изображена на рис.4.
Задание 2. Найти частные производные функции двух переменных 2-го порядка.
а) При нахождении частной производной 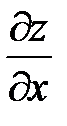 переменная
переменная 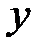 рассматривается как постоянная:
рассматривается как постоянная:
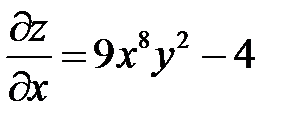 .
.
При нахождении частной производной 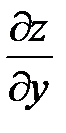 переменная
переменная 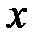 рассматривается как постоянная:
рассматривается как постоянная:
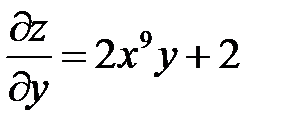 .
.
Найдём частные производные второго порядка:
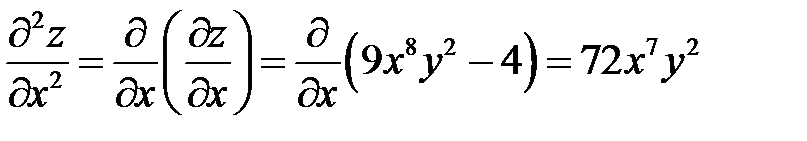 ,
,
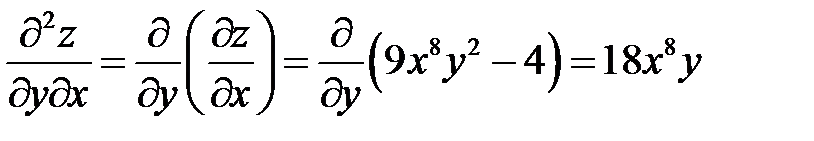 ,
,
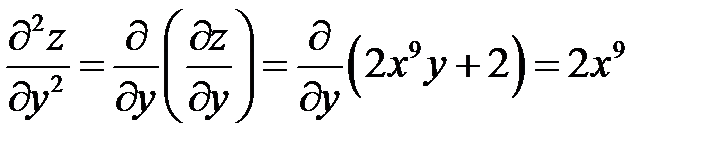 ,
,
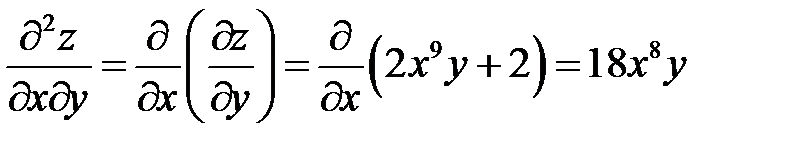 .
.
б) найдём частные производные первого порядка:
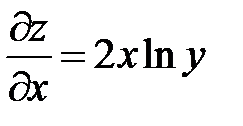 ,
, 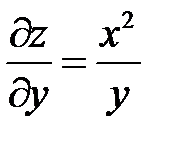 .
.
Найдём частные производные второго порядка:
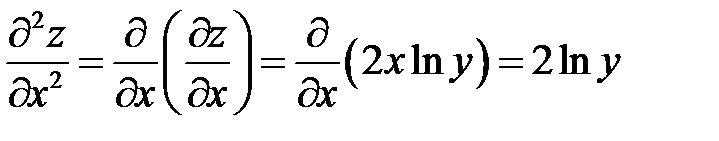 ,
,
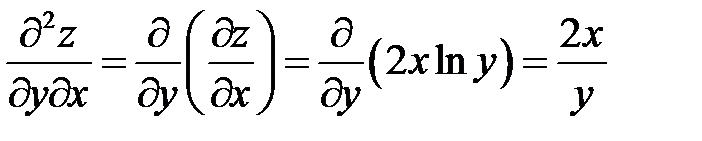 ,
,
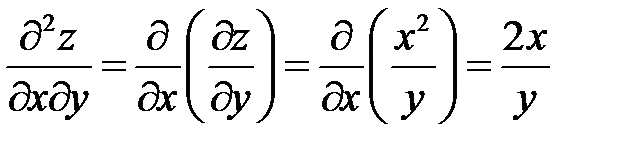 ,
,
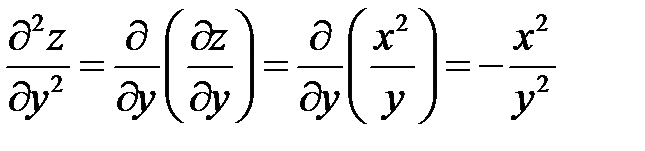 .
.
Задание 3. Исследовать на экстремум функцию 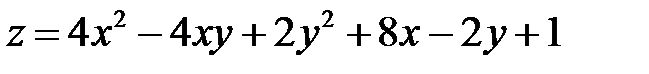 .
.
Вычислим частные производные первого порядка
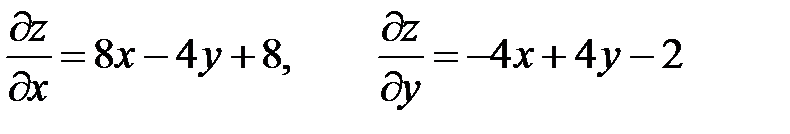
и приравняем их к нулю:
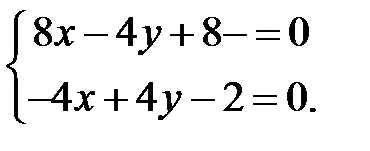
Решая систему уравнений, находим стационарную точку 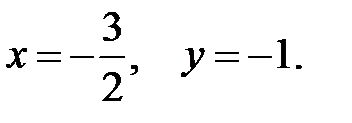 Чтобы определить, действительно ли точка
Чтобы определить, действительно ли точка 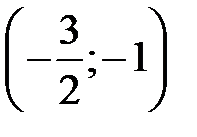 является точкой экстремума, найдём частные производные второго порядка:
является точкой экстремума, найдём частные производные второго порядка:
|
|
|
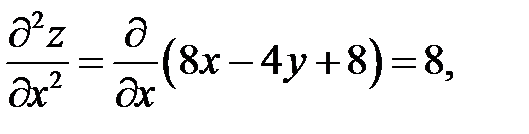
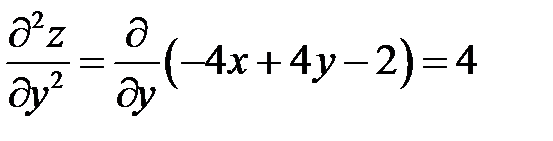 ,
,
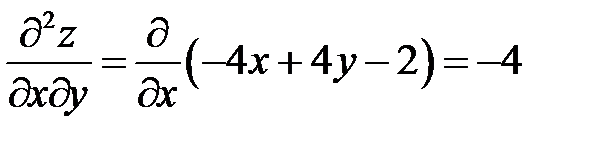 .
.
Так как величина 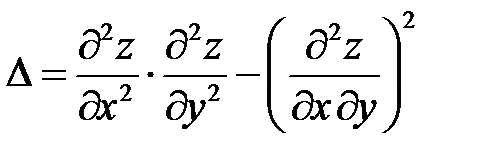 в точке
в точке 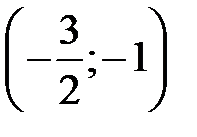 положительна:
положительна:  ,
,
то эта точка является точкой экстремума.
Так как 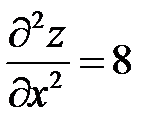 положительна в точке
положительна в точке 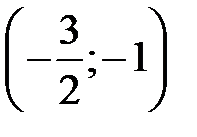 , то точка
, то точка 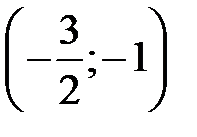
 точка минимума.
точка минимума.
Найдём значение функции в этой точке: 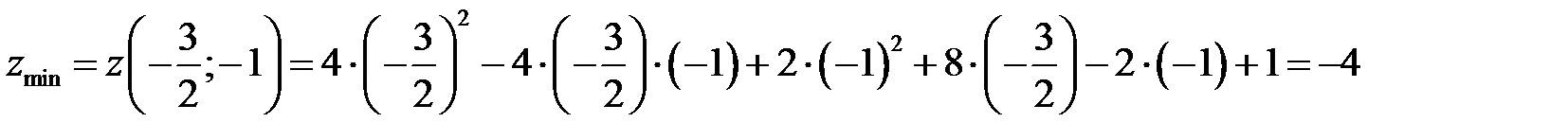
 2020-10-09
2020-10-09 258
258








