2015-07-21
6092
Поэтому не ленимся – ТЕРПЕЛИВО рассматриваем КАЖДЫЙ интервал: из КАЖДОГО интервала берём наиболее выгодную точку и выясняем знак функции в данной точке.
Вот простой пример, когда интервала два, но знакочередования нет: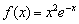 
. Экспонента всегда положительна 
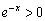, квадрат неотрицателен 
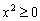, поэтому вся функция неотрицательна: 
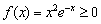, очевидно, достигая нуля в единственной точке 
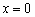. Такого решения будет вполне достаточно. Не обязательно чертить координатную ось! Обратите внимание, здесь есть тонкость при записи ответа:
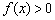, если 
.
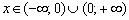То есть, функция положительна везде, кроме точки ноль.
Но формально можно использовать метод интервалов, который приведёт нас к такому же результату:
Если честно, не помню, как выглядит чертёж, однако совершенно точно можно сказать, что график данной функции лежит в верхней полуплоскости и касается оси абсцисс в точке .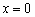
Или парабола, касающаяся оси, например: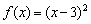 
. Такая же история. Кстати, если вы внимательно изучили геометрические преобразования графиков, то сразу поймёте, как расположена данная парабола.
Следует отметить, что ситуация касания графика оси не единственна, в ряде случаев функция не меняет знак при переходе через точку разрыва. Хороший пример встретился в статье Непрерывность функции: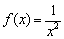 
.
Пример 3
Найти интервалы знакопостоянства функции.
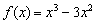
Это пример для самостоятельного решения. После того, как определите знаки на интервалах, попытайтесь представить, как выглядит данная «молния». Примерный образец чистового оформления задания в конце урока.
Функции с многочленами встречаются очень часто, поэтому имеет смысл рассмотреть ещё пару экземпляров:
Пример 4
Найти интервалы знакопостоянства функции.
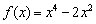
Решение:
1) Функция определена на всей числовой прямой.
2) Находим нули функции:
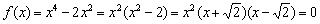
Таким образом, нули функции: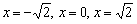 
.
3) Откладываем данные значения на оси абсцисс:
Определим знаки функции на полученных интервалах:
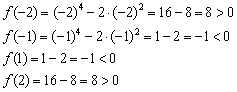
Таким образом:
Ответ:
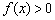, если 
;
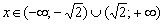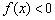, если 
.
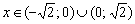Читатели с высоким и средним уровнем подготовки могут укоротить процесс решения, используя чётность/нечётность функций, чайникам же рекомендую не торопиться и тщательно прорабатывать каждый пункт решения.
Многочлен 4-ой степени тоже достоин полного графика:
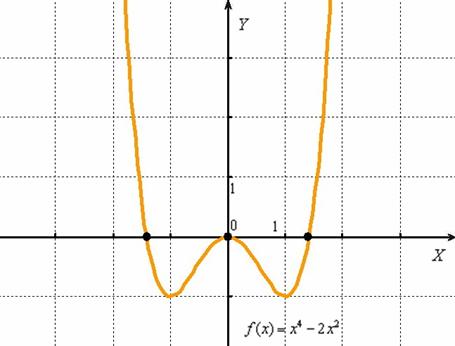
Собрат для самостоятельного решения:
Пример 5
Найти интервалы знакопостоянства функции.
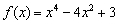
В ходе выполнения задания потребуется решить так называемое биквадратное уравнение, которое также рассматривается в школьном курсе математики. В данном примере необходимо провести замену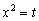 
, разобраться с уравнением 
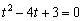, найти корни 
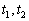и на финише из равенств 
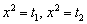получить 4 корня. Полное решение и ответ в конце урока.
Перейдём к обширной группе функций, у которых есть точки разрыва:
Пример 6
Найти интервалы знакопостоянства функции.
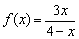
Решение: вот здесь начинает в полную силу работать пункт №1 алгоритма:
1) Функция определена на всей числовой прямой, кроме точки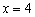 
, которая обращает знаменатель в ноль.
2) Находим точки пресечения графика с осью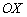 
(нули функции):
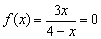
Знаменатель нулевым быть не может, поэтому приравниваем к нулю числитель и решаем уравнение счастливого первоклассника:
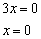
3) Откладываем на оси абсцисс ВСЕ найденные точки, при этом выкалываем точку 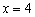, так как она не входит в область определения функции:
Определим знаки функции на полученных интервалах:
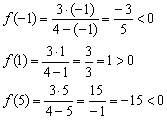
В результате:
Ответ:
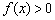, если 
;
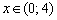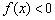, если 
.
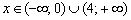Чем отличается данный пример от всех предыдущих? Да ничем особенным.
Напоминаю, что практически так же решается ряд смежных задач, например:
Решить неравенство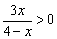 
Ответ: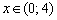
Решить неравенство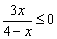 
Ответ: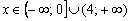 
Найти область определения функции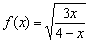 
Ответ: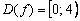 
И т.д.
Короткое разминочное задание для самостоятельного решения:
Пример 7
Найти интервалы знакопостоянства функции.
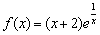
Кстати, подобные вещи вполне реально решить мысленно! Попытайтесь найти интервалы знакопостоянства «в уме», тем более, вы ничем не рискуете – в конце урока есть готовый образец.
Рассмотрим более навороченные дробно-рациональные функции:
Пример 8
Найти интервалы знакопостоянства функции.
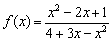
Решение: далее пункты алгоритма нумеровать не будем.
Находим область определения функции. Проверим, обращается ли знаменатель в ноль:
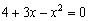
Перепишем квадратное уравнение в привычном виде:
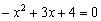
И для удобства сменим знаки у каждого слагаемого:
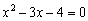
!!! Внимание: в САМОЙ ФУНКЦИИ так делать НЕЛЬЗЯ! В ней знак «минус» не пропадает: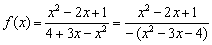 
.
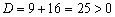
Дискриминант больше нуля, значит, уравнение имеет два действительных корня и в область определения не войдут две точки:
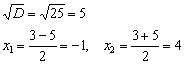
Найдём точки пересечения графика с осью абсцисс: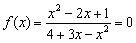 
. Нулевым может быть только числитель, поэтому рассматриваем уравнение 
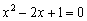. Решение можно провести через дискриминант, однако нетрудно заметить, что у нас квадрат разности:
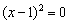
Таким образом, функция обращается в ноль в единственной точке: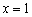 
Используя уже наработанный алгоритм, определим знаки функции на полученных интервалах:
Ответ:
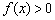, если 
;
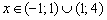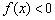, если 
.
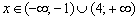Как выглядит график функции, знают немногие, но совершенно точно можно сказать, что на интервалах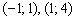 
он расположен ВЫШЕ оси 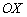, а на интервалах 
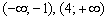– НИЖЕ данной оси. В точке 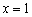график, кстати, только касается её.
Пример 9
Найти интервалы знакопостоянства функции.
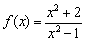
Это пример для самостоятельного решения.
Заключительные примеры посвящены функциям, в которые входит натуральный логарифм:
Пример 10
Найти интервалы знакопостоянства функции.
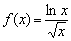
Просто и со вкусом.
Решение: функция определена и непрерывна на интервале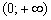 
. Найдём точки пересечения графика с осью абсцисс:
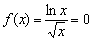
Нулю может быть равен только числитель:
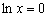
Согласно определению логарифма (которое нужно бы уже хорошо усвоить):
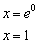
Отметим найденные точки на числовой прямой:
На промежутке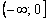 
функция не определена вообще. Об этом можно сделать пометку на чертеже либо просто оставить полуинтервал без внимания. Я обычно не ставлю никаких знаков.
Определим знаки на интервалах, которые входят в область определения функции:
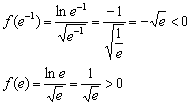
Таким образом:
Ответ:
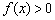, если 
;
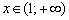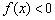, если 
.
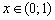На практике под логарифмом часто находится квадратный дву- или трёхчлен. Пожалуйста, ВНИМАТЕЛЬНО изучите оставшиеся примеры, в которых метод интервалов используется ДВАЖДЫ: первый раз для нахождения области определения, а второй раз для нахождения интервалов знакопостоянства.
Пример 11
Найти интервалы знакопостоянства функции.
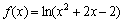
Решение: сначала найдём область определения функции. Выражение под знаком логарифма должно быть положительным:
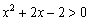
Квадратичное неравенство решим методом интервалов. Проверим, существуют ли действительные корни соответствующего уравнения:
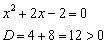
Да, уравнение имеет два действительных перца. Не нужно удивляться, что дискриминант получился «плохой», это довольно распространённый инцидент в ходе исследовании функций. Невозмутимо находим корни:
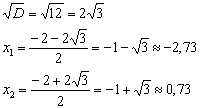
Откладываем найденные точки на числовой прямой. Их следует выколоть, поскольку неравенство строгое. Далее стандартно из каждого интервала выбираем наиболее простую точку, и определяем знаки функции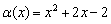 
на полученных интервалах:
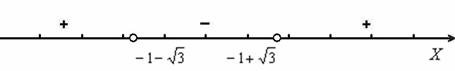
Таким образом, область определения:
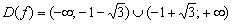
Что теперь? Теперь ЗАБЫВАЕМ про найденные знаки и интервалы знакопостоянства. Самый важный факт состоит в том, что отрезок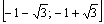
не входит в область определения функции 
.
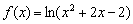На втором шаге находим точки пересечения графика с осью абсцисс (нули функции):
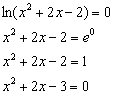
Решаем ещё одно квадратное уравнение:
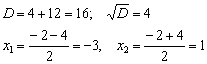
Снова используем метод интервалов. Откладываем на числовой прямой ВСЕ найдённые ранее точки:
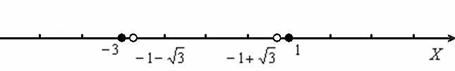
Тесновато получилось, но что делать, зато масштаб выдержан.
Определяем знаки функции на интервалах, при этом не забываем, что отрезок посередине не входит в область определения, и возиться с ним не надо! Но от этого, увы, не легче, так как подстановка будет брутальной. Придётся тыкать по клавишам калькулятора:
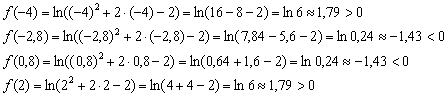
Таким образом:
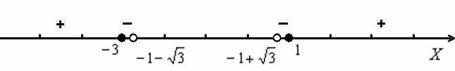
Ответ:
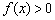, если 
;
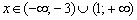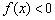, если 
.
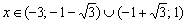Что можно сказать о графике функции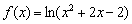 
? На отрезке 
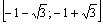его не существует вообще, на крайних интервалах он расположен выше оси 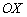, на маленьких интервалах – ниже данной оси, точки пересечения с осью: 
.
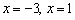Пример 12
Найти интервалы знакопостоянства функции.
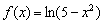
Это пример для самостоятельного изучения. На первом шаге решение можно ускорить – неравенство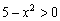 
значительно выгоднее решить аналитически, нежели использовать метод интервалов. Данный способ подробно рассмотрен на уроке Область определения функции.
Вот, пожалуй, и все основные задания по теме, которые встречаются на практике в ходе полного исследования функции. Хочется привести примеры сложнее, но они будут в известной степени надуманы.
Желаю успехов!
Решения и ответы:
Пример 3: Решение:
1) Функция определена на всей числовой прямой.
2) Найдём нули функции:
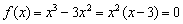
Таким образом: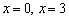 
.
3) Определим знаки функции методом интервалов:
Ответ:
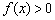, если 
;
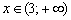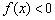, если 
.
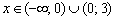Пример 5: Решение:
1) Функция определена на всей числовой прямой
2) Найдём нули функции:
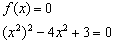
Проведём замену: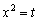 
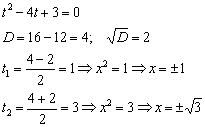
3) Выполним чертёж и определим знаки функции на найденных интервалах:
Ответ:
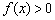, если 
;
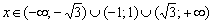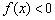, если 
.
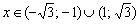Пример 7: Решение:
1) Функция определена на всей числовой прямой, кроме точки .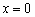
2) Найдём нули функции:
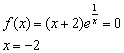
3) Определим знаки функции на полученных интервалах:
Ответ:
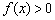, если 
;
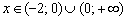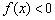, если 
.
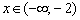Пример 9: Решение: точки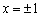 
не входят в область определения функции.
График функции не пересекает ось 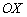, т.к.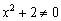 
Методом интервалов определим знаки функции:
Ответ:
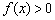, если 
;
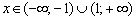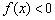, если 
.
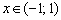Пример 12: Решение: найдём область определения:
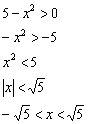
Таким образом,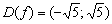 
Найдём точки пересечения графика с осью абсцисс:
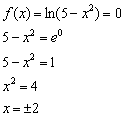
Определим знаки функции на полученных интервалах:
Ответ:
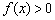, если 
;
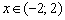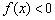, если 
.
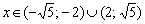Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Что такое производная?
Определение и смысл производной функции
Многие удивятся неожиданному расположению этой статьи в моём авторском курсе о производной функции одной переменной и её приложениях. Ведь как оно было ещё со школы: стандартный учебник в первую очередь даёт определение производной, её геометрический, механический смысл. Далее учащиеся находят производные функций по определению, и, собственно, только потом оттачивается техника дифференцирования с помощью таблицы производных.
Но с моей точки зрения, более прагматичен следующий подход: прежде всего, целесообразно ХОРОШО ПОНЯТЬ предел функции, и, в особенности, бесконечно малые величины. Дело в том, что определение производной базируется на понятии предела, которое слабо рассмотрено в школьном курсе. Именно поэтому значительная часть молодых потребителей гранита знаний плохо вникают в саму суть производной. Таким образом, если вы слабо ориентируетесь в дифференциальном исчислении либо мудрый мозг за долгие годы успешно избавился от оного багажа, пожалуйста, начните с пределов функций. Заодно освоите/вспомните их решение.
Тот же практический смысл подсказывает, что сначала выгодно научиться находить производные, в том числе производные сложных функций. Определение определением, смысл смыслом, а дифференцировать, как говорится, хочется всегда. В этой связи лучше проработать перечисленные базовые уроки, а может и стать мастером дифференцирования, даже не осознавая сущности своих действий.
Более того, многие приложения производной не требуют её понимания, в частности, ряд простейших задач с производной или приближенные вычисления с помощью дифференциала. Неудивительно, что данный урок появился достаточно поздно – в ходе разработки темы «Функции и графики», когда мне потребовалось объяснять нахождение интервалов возрастания/убывания и экстремумов функции.
Поэтому, уважаемые чайники, не спешите набрасываться на материалы странички как голодные звери, ибо насыщение будет невкусным и, как следствие, неполным.
