Определение. Квадратным уравнением называют уравнения вида
a х2 + bx + c = 0, где коэффициенты a, b, c любые действительные числа, причём 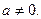
D = b2 – 4 a c называют дискриминантом квадратного уравнения.
Если D>0, то уравнение имеет два корня, которые находятся по формулам х1,2 = 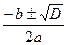 (х1 =
(х1 = 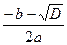 , х2 =
, х2 = 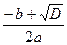 ).
).
Если D=0, то уравнение имеет один корень, который находится по формуле х = 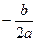 .
.
Если D<0, то уравнение не имеет корней.
Решим квадратные уравнения:
а) 3х2 + 8х – 11 = 0.
Решение: а = 3, b = 8, с = -11.
D = b2 – 4ас = 82 – 4.3.(-11) = 64 + 132 = 196.
х1,2 = 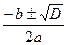 =
= 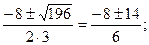
х1 = 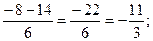
х2 = 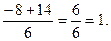
Ответ: 1; 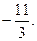
б) 2х2 + 4х + 7 = 0.
Решение: а = 2, b = 4, с = 7.
D = b2 – 4ас = 42 – 4.2.7 = 8 - 56 = -40 <0.
Так как D<0, данное уравнение не имеет корней.
в) 4х2 - 20х + 25 = 0.
Решение: а = 4, b = -20, с = 25.
D = b2 – 4ас = (-20)2 – 4.4.25 = 400 - 400 = 0.
х1,2 = 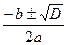 =
= 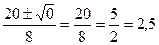 . Ответ: 2,5.
. Ответ: 2,5.
Решите уравнение:
1) х2 + 6х + 8 = 0; 2) х2 - 5х + 6 = 0; 3) х2 - 2х - 15 = 0;
4) x 2 + 6 x – 40 = 0; 5) x 2 + x – 2 = 0; 6) х2 - 3х - 18 = 0; 7) х2 + 4х + 4 = 0; 8) х2 - 6х + 9 = 0; 9) 2х2 + 3х + 1 = 0;
10) 3х2 - 3х + 4 = 0; 11) 5х2 - 8х + 3 = 0; 12) 14х2 - 5х - 1 = 0;
13) 4х2 + 10х - 6 = 0; 14) 14х2 - 5х - 1 = 0; 15) 3х2 - 8х + 5 = 0;
16) 4х2 - 12х + 9 = 0; 17) 5 х 2 + 8 х – 4 = 0; 18) 5 х 2 + 14 х – 3 = 0;
19) 7 х 2 – 9 х – 10 = 0; 20) 7 х 2 – 18 х – 9 = 0; 21) х2 = 2х + 48;
22) 6х2 + 7х = 5; 23) х2 = 4х + 96; 24) 2х2 – 2 = 3х;
25) -х2 = 5х - 14; 26) -3х2 +5 = 2х; 27) 25 = 26х – х2;
28) -5х2 = 9х - 2; 29) х2 + 7х + 2 = 0; 30) 2х2 + 3х – 1 = 0.
2. Найдите корни уравнения:
1) (х + 4)2 + (х + 4) – 12 = 0;. 2) (х – 3)2 – 2(х – 3) – 15 = 0;
3) (х + 3)2 – 2(х + 3) – 8 = 0; 4) (х – 5)2 + 3(х – 5) – 10 = 0;
5) (х – 2)2 = 3х – 8; 6) (х + 3)2 = 2х + 6;
7) (х – 1)2 = 29 – 5х; 8) (х + 2)2 = 43 – 6х;
9) 5(х + 2)2 = -6х – 44; 10) 4(х – 1)2 = -12х + 3;
11) (х + 3)2 -16 = (1 - 2х)2; 12) (х – 2)2 + 24 = (2 + 3х)2;
13) (х – 2)(х + 2) = 7х – 14; 14) (х – 3)(х + 3) = 5х – 13;
15) (-х – 1)(х - 4) = х (4х – 11); 16) (х + 4)(2х - 1) = х (3х + 11);
17) -х (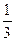 – х) = (х - 1)(х + 1); 18) -х (4х + 1) = (х + 1)(х - 2);
– х) = (х - 1)(х + 1); 18) -х (4х + 1) = (х + 1)(х - 2);
39) 5(х - 2) = (х - 2)(3х + 2); 40) 7(1 - х) = (2х + 3)(1 – х);
41) 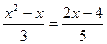 ; 42)
; 42) 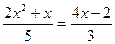 ; 43)
; 43) 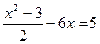 ;
;
44) 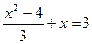 ; 45)
; 45) 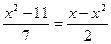 ; 46)
; 46) 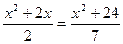 ;
;
47) 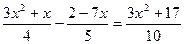 ; 48)
; 48) 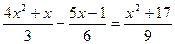
 2015-04-08
2015-04-08 2533
2533
