Используя разложение функций в степенные ряды Тейлора и Маклорена, можно приближенно вычислять, например, значения функций и приближенные значения определенных интегралов.
Напомним, что рядом Тейлора для функции 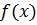 , если функция определена в окрестности точки
, если функция определена в окрестности точки 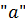 и имеет в этой точке конечные производные, является степенной ряд:
и имеет в этой точке конечные производные, является степенной ряд:
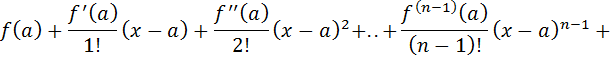
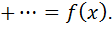
Чтобы функция 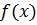 была суммой этого ряда для значений x из некоторого промежутка, необходимо и достаточно, чтобы
была суммой этого ряда для значений x из некоторого промежутка, необходимо и достаточно, чтобы 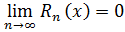 , где
, где 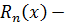 остаточный член ряда.
остаточный член ряда.
Если в ряде Тейлора положить 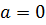 , то получим ряд Маклорена:
, то получим ряд Маклорена:
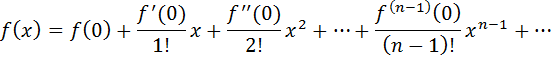
Обычно в задачах на приближенные вычисления используются ряды Маклорена для следующих функций:
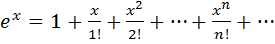 , область сходимости этого степенного ряда к своей функции - (-∞; +∞).
, область сходимости этого степенного ряда к своей функции - (-∞; +∞).
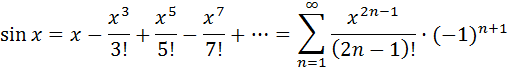
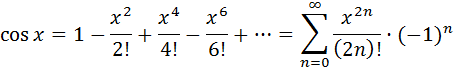
Области сходимости последних двух рядов также (-∞; +∞).
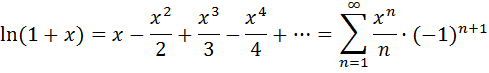
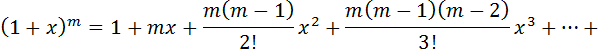
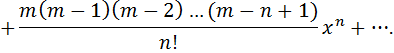
Можно показать, что область сходимости последних двух рядов 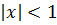 .
.
При 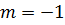 , из последней формулы получим:
, из последней формулы получим: 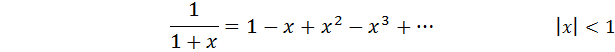
Если же x заменить на (-x) то получим формулу суммы бесконечно убывающей геометрической прогрессии:
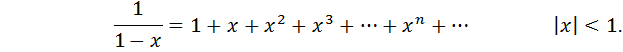
Пример: вычислить приближенно 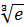 , взяв три члена разложения; оценить погрешность вычислений.
, взяв три члена разложения; оценить погрешность вычислений.
Воспользуемся разложением в ряд Маклорена функции 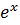 , положив
, положив 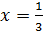 .
.
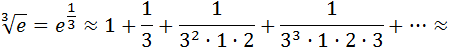
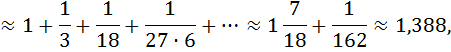
Погрешность вычислений: 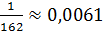
Если в задаче указано число членов разложения, то погрешностью вычислений будет первый отбрасываемый член разложения, в данном случае, - четвертый.
Пример: вычислить 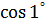 с точностью до
с точностью до 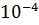 .
.
Воспользуемся разложением функции 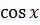 в ряд, предварительно переведя один градус в радианную меру
в ряд, предварительно переведя один градус в радианную меру
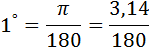
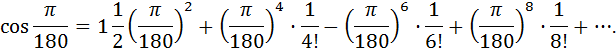
Оценим каждое слагаемое, начиная со второго. Как только слагаемое будет меньше заданной точности, оно в приближенную сумму не будет входить.
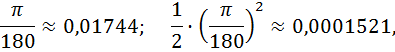
следовательно,
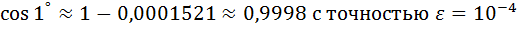
Пример: вычислить приближенно определенный интеграл с точностью 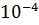 .
.
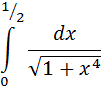
Разложим подынтегральную функцию 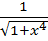 в степенной ряд
в степенной ряд
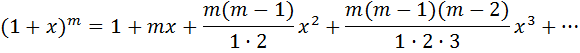
В нашем случае 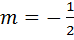 , вместо x подставляя
, вместо x подставляя 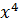 , получим:
, получим:
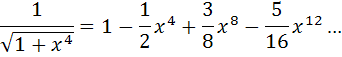
Вместо заданной подынтегральной функции будем интегрировать в заданных пределах степенной ряд. Отбрасывая третий и последующие члены ряда, после подстановки пределов интегрирования, получим:
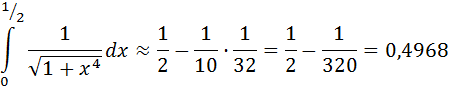
Т.к. после интегрирования третий член ряда равен 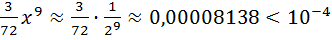 , то погрешность вычислений равна
, то погрешность вычислений равна 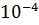 .
.
Пример: вычислить определенный интеграл с точностью до 0.001
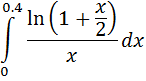
Воспользуемся разложением
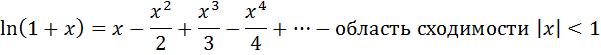
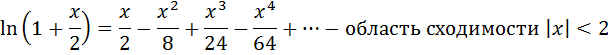
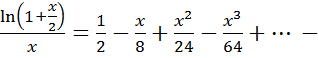 преобразовали подынтегральную функцию, тогда:
преобразовали подынтегральную функцию, тогда:
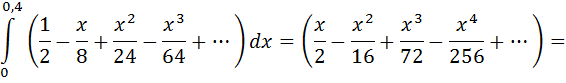
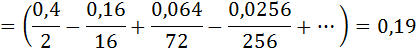
Т.е. приближенно данный определенный интеграл равен 0,19. Точность вычислений 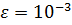 .
.
 2015-04-08
2015-04-08 19038
19038
