Закон теплопроводности Фурье

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА

ТЕПЛОПРОВОДНОСТИ МАТЕРИАЛОВ МЕТОДОМ

ЦИЛИНДРИЧЕСКОГО СЛОЯ.

Методические указания

к лабораторной работе №1

по дисциплине «Процессы и аппараты пищевых производств»

Ижевск 2009

Методические указания разработаны на основе Государственного образовательного стандарта высшего профессионального образования. Рассмотрено и рекомендовано к изданию редакционно-издательским советом ФГОУ ВПО «Ижевская ГСХА», протокол №______ от ______________.

Издание исправленное и дополненное

Рецензент:

Доцент каф. ТМППЖ Васильченко М.Ю.

Сергеев А.А.

Определение теплопроводности материалов методом цилин-

дрического слоя: Методические указания./ А.А. Сергеев.-

Ижевск: ИжГСХА, 2009.- 12 с.

© Сергеев А.А., 2009

Основные положения.

Закон теплопроводности Фурье.

Рассмотрим слой твердого вещества, заключенного между двумя параллельными пластинами, которые отстоят на расстоянии Х одна от другой. Предположим, что первоначально вещество находилось при температуре t_0. В момент времени t = 0 температура нижней пластины внезапно повышается до значения t₁. Это значение поддерживается на нижней пластине во все последующие моменты времени. В результате профиль температур внутри слоя начинает деформироваться во времени, и при достаточно больших значениях t устанавливается стационарное линейное распределение температуры. В стационарных условиях для поддержания разности температур Dt = t₁ - t₀ в слое площадью F требуется наличие постоянного теплового потока Q. При достаточно малых значениях Dt справедливо соотношение

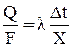, (1.1)

согласно которому скорость переноса теплоты через единицу поверхности слоя пропорциональна перепаду температуры на расстоянии Х.

Коэффициент пропорциональности l называют коэффициентом теплопроводности (или просто теплопроводностью) материала.

Теплопроводностью называют процесс распространения теплоты между частицами тела, находящимися в соприкосновении; при этом тепловая энергия передается внутри тела от одних частиц к другим вследствие их колебательного движения.

Уравнение (1.1) справедливо также в тех случаях, когда пространство между параллельными пластинами заполнено не твердым веществом, а жидкостью или газом при условии, что приняты все необходимые меры по устранению конвекции и излучения. Таким образом, это соотношение описывает процесс теплопроводности в твердых телах, жидкостях и газах.

Представим выражение (1.1) в дифференциальной форме. С этой целью запишем его для предельного случая, когда толщина слоя стремится к нулю. Если локальную скорость переноса теплоты через единицу поверхности слоя (тепловой поток) в положительном направлении оси х обозначить через q_х, то в дифференциальной форме соотношение (1.1) будет иметь вид

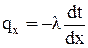(1.2)

Это уравнение представляет собой одномерную формулировку закона теплопроводности Фурье. Оно справедливо, если температура зависит только от одной координаты х. Следовательно, закону теплопроводности может быть дана следующая формулировка: