Требования к математическим моделям

Математические модели предъявляют общие требования точности, экономичности, универсальности.

Точность ММ — это ее свойство, отражающее степень совпадения предсказанных с помощью моделей значений параметров объекта с истинными значениями этих парамет­ров.

Количественная оценка точности модели вызывает за­труднения по следующим причинам:

1) Реальные объекты и их модели характеризуются не одним, а несколькими параметрами, отсюда вытекает век­торный характер оценки точности и необходимость сведения векторной оценки точности и скалярной для возможности сопоставления моделей друг с другом.

2) Модели сравниваются для многократного использова­ния при анализе разных вариантов объекта проектирования или многих типов объектов определенного класса. Напри­мер, математическая модель транзистора применяется при анализе транзисторных схем разных типов, с транзисторами разных марок и т. д. Поскольку характер проявления тех

или иных свойств объекта зависит от особенностей взаимо­связи объекта с внешней средой и другими объектами систе­мы, то и показатели отображения этих свойств в математи­ческой модели будут зависеть от конкретных условий функ­ционирования объектов. В результате оценка точности перестает быть однозначной.

3) Истинные значения параметров объекта проектирова­ния отождествляются с экспериментально полученными, од­нако погрешности эксперимента во многих случаях оказы­ваются соизмеримыми с погрешностями математической модели, а иногда заметно их превышают. Для получения значений близких к истинным с помощью более точных ма­тематических моделей, чем испытуемые, требуется наличие такой более точной модели, что выполняется не всегда.

Сведение векторной оценки к скалярной осуществляется двумя путями:

Пусть объект характеризуется параметрами:

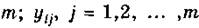
А значения тех же параметров, полученные при испыта­нии моделей, —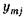

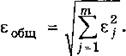
Для оценки точности будем использовать или т-норму (максимальный по абсолютной величине элемент вектора:

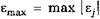, где 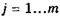) или 1-норму:

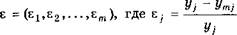
Образуем векторы относительных погрешностей

Для того чтобы уменьшить влияние неопределенности, вызываемое вторым фактором, целесообразно проводить сравнение моделей по результатам их использования в неко­торых стандартных ситуациях. Эти ситуации называются тестовыми, ограниченное количествово тестовых ситуаций упрощает исследования с целью получения значений у, до­статочно близких к истинному (рис. 3.13).

Экономичность математических моделей в САПР опре­деляется прежде всего затратами машинного времени на

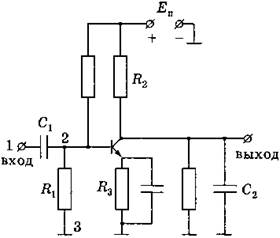
Рис. 3.13. Пример тестовой схемы для сравнения программ схемотехнического моделирования

решение задач, ее можно также оценивать количеством арифметических операций, выполняемых при однократной реализации уравнений моделей. Кроме того, показателем экономичности математической модели может служить также количество используемых в ней внутренних пара­метров.

Степень универсальности определяется ее применимо­стью к анализу достаточно большой группы однотипных объектов в одном или нескольких режимах работы. Требо­вание высокой точности, большой степени универсальности с одной стороны и высокой экономичности с другой проти­воречиво, поэтому для одного и того же элемента необходи­мо иметь несколько математических моделей, различаю­щихся значениями показателей эффективности.