План лекции:
1) Пересечение множеств.
3) Разность множеств.
4) Симметрическая разность.
5) Дополнение множеств.
6) Декартово (прямое) произведение двух множеств.

1. Пересечением множеств А и В называется множество, состоящее из элементов, которые принадлежат множествам А и В одновременно.
Пересечение множеств А и В обозначают: А Ç В.
А Ç В = {х| хÎА и хÎВ}
Если представить множества А и Впри помощи кругов Эйлера, то пересечение данных множеств изобразится заштрихованной областью (рис. 1).
В том случае, когда множества А и В не имеют общих элементов, то говорят, что их пересечение пусто и пишут: А Ç В = Æ.
А Ç Æ = Æ.
Если ВÌ А, то А Ç В = В.
Операция, при помощи которой находят пересечение множеств, называется также пересечением.
Пример.
1) А ={1, 2, 3, 4, 5}; В = {4, 5, 6, 7}
А Ç В = {4, 5}
2) Пересечением множества прямоугольников и множества ромбов является множество квадратов.
3) Пересечением множества чётных чисел и множества нечётных чисел пусто.

2. Объединением множеств А и В называется множество, состоящее из элементов, которые принадлежат хотя бы одному из множеств А и В.
Объединение множеств А и В обозначают: А È В.
А È В = {х| хÎА или хÎВ}
Если представить множества А и В при помощи кругов Эйлера, то объединение данных множеств изобразится заштрихованной областью (рис. 2).
Если ВÌ А, то А È В = А.
А È Æ = А.
Операция, при помощи которой находят объединение множеств, называется также объединением.
Пример.
1) А = {1, 2, 3, 4, 5}; В = {4, 5, 6, 7}
А È В = {1, 2, 3, 4, 5, 6, 7}
2) Объединение множества положительных чётных чисел и множества положительных нечётных чисел является множество натуральных чисел.
Если в выражении есть Ç и È множеств, но нет скобок, то сначала выполняют Ç.
Операции пересечения и объединения множеств обладают свойствами:
1° Коммутативность пересечения
"А, В А Ç В = В Ç А
2° Коммутативность объединения
"А, В А È В = В È А
3º Ассоциативность пересечения
"А, В, С (А Ç В) Ç С = А Ç (В Ç С)
4º Ассоциативность объединения
"А, В, С (А È В) È С = А È (В È С)
5º Пересечение дистрибутивно относительно объединения
"А, В, С А Ç (В È С) = (А Ç В) È (А Ç С)
6º Объединение дистрибутивно относительно пересечения
"А, В, С А È (В Ç С) = (А È В) Ç (А È С)
7º "А А Ç А = А
8º "А А È А = А
Доказательство:
Справедливость каждого из этих утверждений можно проверить, показав, что множество, стоящее по одну сторону от знака равенства, включено в множество, стоящее по другую сторону от этого знака.
Например, докажем свойство 6º.
а) Докажем, что А È (В Ç С) Ì (А È В) Ç (А È С).
Пусть х Î А È (В Ç С). Тогда х Î А или х Î (В Ç С).
Если х Î А, то х Î А È В и х Î А È С, а, следовательно, х Î (А È В) Ç (А È С).
Если х Î (В Ç С), то х Î В и х Î С. Следовательно, х Î А È В и х Î А È С, т.е. и в этом случае х Î (А È В) Ç (А È С).
б) Докажем, что (А È В) Ç (А È С) Ì А È (В Ç С).
Пусть х Î (А È В) Ç (А È С). Тогда х Î А È В и х Î А È С.
То есть, (х Î А или х Î В) и (х Î А или х Î С).
Значит, х Î А или (х Î В и х Î С), т.е. х Î А È (В Ç С).
Проиллюстрируем свойство 6º на диаграммах Эйлера–Венна.
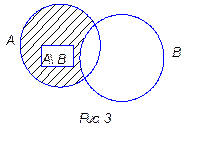
3. Разностью множеств А и В называется множество, элементы которого принадлежат множеству А и не принадлежат множеству В.
 Обозначают А \ В; А – В.
Обозначают А \ В; А – В.
А \ В = { х| хÎА и хÏВ }
Если представить множества А и В при помощи кругов Эйлера, то разность данных множеств изобразится заштрихованной областью (рис. 3).
Операция, при помощи которой находят разность множеств, называется вычитанием.
Пример.
1) А = {1, 2, 3, 4, 5}; В = {4, 5, 6, 7}
А \ В = {1, 2, 3}
2) Разностью множества чётных чисел и множества целых чисел является пустое множество.
4. Симметрической разностью множеств А и В называется множество, состоящее из элементов, принадлежащих только множеству А или только множеству В.

Симметрическую разность множеств А и В обозначают: А х В; А – В.
А х В = { х| хÎА, хÏВ или хÏА, хÎВ}
Если представить множества А и В при помощи кругов Эйлера, то симметрическая разность данных множеств изобразится заштрихованной областью (рис. 4).
А х В = (А \ В) È (В\ А)
А х В = (А È В) \ (А Ç В)
5. Универсальным множеством U (основным множеством) называется множество, для которого все множества, рассматриваемые в данный момент, являются подмножествами.
Универсальное множество часто изображают прямоугольником.
Например, для N универсальным считается множество Z.
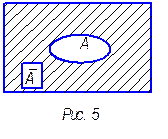
Дополнением множества А называется разность между универсальным множеством и множеством А.
Дополнение множества А обозначают 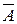 .
.
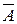 = U \ A = {хÏА}
= U \ A = {хÏА}
При помощи кругов Эйлера дополнение изображается рис. 5.
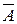 È А = U
È А = U 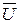 = Æ
= Æ
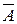 Ç А = Æ = U
Ç А = Æ = U
Пример.
1) А = {2k}; U = Z ® 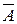 = Z \ A = {2k+1}.
= Z \ A = {2k+1}.
Операции разности и дополнения множеств обладают свойствами:
9º Разность антидистрибутивна относительно пересечения. "А, В, С
А \ (В Ç С) = (А \ B) È (A \ C)
10º Разность антидистрибутивна относительно объединения. "А, В, С
А \ (В È С) = (А \ B) Ç (A \ C)
11º (частный сл. 9º) Дополнение пересечения А и В равно объединению дополнений А и В.
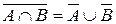
12º (частный сл. 10º) Дополнение объединения А и В равно пересечению дополнений А и В.
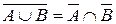
Докажем св. 9º и проиллюстрируем его на диаграммах Эйлера–Венна.
а) Докажем, что А \ (В Ç С) Ì (А \ B) È (A \ C).
Пусть х Î А \ (В Ç С).
Тогда х Î А и х Ï (В Ç С), т.е. или х Ï В, или х Ï С.
Значит, или (х Î А и х Ï В), или (х Î А и х Ï С), т.е. х Î А \ B или хÎА\ С.
Т.е. х Î(А \ B) È (A \ C).
б) Докажем, что (А \ B) È (A \ C) Ì А \ (В Ç С).
Пусть х Î (А \ B) È (A \ C).
Тогда х Î (А \ B) или х Î (A \ C), т.е. (х Î А и х Ï В) или (х Î А и х Ï С)
Значит, х Î А и (х Ï В и х Ï С), т.е. х Î А \ (В Ç С).
Дом. задание. Доказать и проиллюстрировать на диаграммах Эйлера–Венна свойства 1 – 5, 7 – 12.
Задание. Найти пересечение, объединение, разность и симметрическую разность множеств А и В, если А = {хÎ R ½–1£ х < 4}, B = { хÎ R ½ 2 < x £ 6}
А Ç В = {хÎ R ½2 < x < 4},
А È В = {хÎ R ½–1 £ x £ 6},
А \ B = {хÎ R ½–1 £ x £ 2},
В \ А = {хÎ R ½4 £ x £ 6},
А? В = {хÎ R ½–1 £ x < 2, 4 < x £ 6}.
 2015-07-21
2015-07-21 22685
22685