Содержание
| Введение | |
| Раздел 1 Элементы линейной алгебры | |
| 1.1 Матрица, виды матриц. Операции над матрицами. Элементы матрицы. Обратная матрица | |
| 1.2 Решение систем линейных уравнений | |
| Раздел 2. Элементы векторной теории | |
| 2.1 Приложение векторной теории к решению задач | |
| 2.2 Прямая линия и её уравнения | |
| 2.3 Решение систем линейных неравенств графическим методом | |
| Раздел 3 Математическое программирование | |
| 3.1 Основные определения | |
| 3.2 Выпуклые множества точек | |
| 3.3 Примеры математических моделей задач линейного программирования | |
| 3.3.1 Задача об использовании или распределении ресурсов | |
| 3.3.2 Задача составления смесей | |
| 3.3.3 Транспортная задача | |
| 3.4 Каноническая или основная задача линейного программирования | |
| 3.5 Методы решений задач линейного программирования | |
| 3.5.1 Графический метод | |
| 3.5. 2 Симплекс-метод | |
| 3.6 Двойственность в линейном программировании | |
| 3.7 Транспортная задача | |
| 3.7.1 Условия оптимальности плана транспортной задачи | |
| 3.7.2 Построение системы потенциалов и проверка плана на оптимальность | |
| 3.7.3 Перераспределение поставок | |
| 3.7.4 Открытая транспортная задача | |
| Список использованных источников |
Раздел 1 Элементы линейной алгебры
Матрица, виды матриц. Операции над матрицами. Элементы матрицы. Обратная матрица
Определение: Матрицей называется прямоугольная таблица чисел, состоящая из m одинаковой длины строк или n одинаковой длины столбцов.

aij- элемент матрицы, который находится в i-ой строке и j-м столбце.
Основные виды матрицы:
- квадратная (это матрица с равным числом столбцов и строк);
- транспонированная (можно получить, поменяв строки и столбцы матрицы местами. Матрица A размера
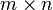 при этом преобразовании станет матрицей AT размерностью
при этом преобразовании станет матрицей AT размерностью 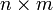 );
); - единичная (квадратная матрица, элементы главной диагонали которой равны единице, а остальные равны нулю)

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Для матрицы определены следующие алгебраические операции:
- сложение матриц, имеющих один и тот же размер;
- умножение матриц подходящего размера (матрицу, имеющую столбцов, можно умножить справа на матрицу, имеющую строк);
- в том числе умножение на матрицу вектора (по обычному правилу матричного умножения; вектор является в этом смысле частным случаем матрицы).
Рассмотрим операции над матрицами более подробно.
1. Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен 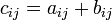
2. Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен 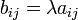
3. Умножение матриц (обозначение: AB, реже со знаком умножения 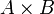 ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго
) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго 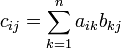 (умножение строки на столбец).
(умножение строки на столбец).
Количество столбцов в матрице A должно совпадать с количеством строк в матрице B. Если матрица A имеет размерность 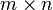 , матрица B —
, матрица B — 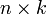 , то размерность их произведения AB = C есть
, то размерность их произведения AB = C есть  . Смотри рис.1.
. Смотри рис.1.
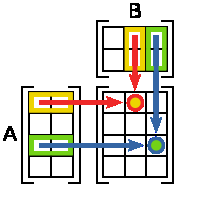
Рисунок 1 - Правило умножения двух матриц
Пример 1: Найти А+2В, если 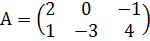 ,
, 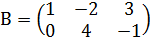 .
.
Решение: 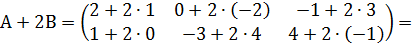
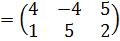
Пример 2: Найти 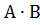 , если
, если 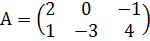 ,
, 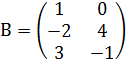
Решение: 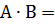
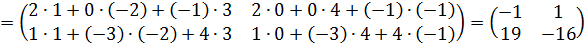
Пример 3: Решить матричное уравнение: 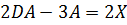 ,
,
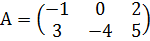 ,
, 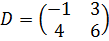
Решение: 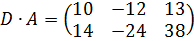 ,
, 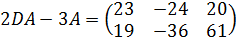 ,
, 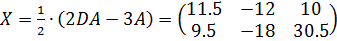
Определение: Определитель матрицы А обозначается как: det(A), |А| или ΔA.
Формула для вычисления определителя второго порядка:
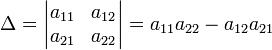
Формулы для вычисления определителя третьего порядка:
а) разложение по элементам первой строке: 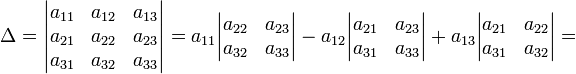
= a11a22a33 − a11a23a32 − a12a21a33 + a12a23a31 + a13a21a32 − a13a22a31;
б) по правилу звездочки (или Саррюса)
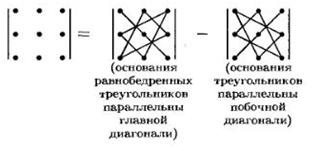
Основные свойства определителей.
Свойство 1. Определитель не изменяется при транспонировании, т.е.
Замечание. Следующие свойства определителей будут формулироваться только для строк. При этом из свойства 1 следует, что теми же свойствами будут обладать и столбцы.
Свойство 2. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е.
Свойство 3. Определитель, имеющий нулевую строку, равен 0.
Свойство 4. Определитель, имеющий две равные строки, равен 0.
Свойство 5. Определитель, две строки которого пропорциональны, равен нулю.
Свойство 6. При перестановке двух строк определителя он умножается на —1.
Свойство 7. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.
Определение 8. Минором, соответствующим данному элементу aij определителя третьего порядка, называется определитель второго порядка, полученный из данного вычёркиванием строки и столбца, на пересечении которых стоит данный элемент, т.е. i-ой строки и j-го столбца. Миноры соответствующие данному элементу aij будем обозначать Mij.
Пример 4: минором M12, соответствующим элементу a12, будет определитель 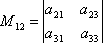 , который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца.
, который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца.
Определение. Алгебраическим дополнением элемента aij определителя называется его минор Mij, умноженный на (–1)i+j. Алгебраическое дополнение элемента aij обозначается Aij.
Из определения получаем, что связь между алгебраическим дополнением элемента и его минором выражается равенством Aij = (–1)i+jMij.
Например, 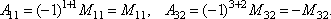
Пример 5: Дан определитель 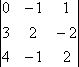 . Найти A13, A21, A32.
. Найти A13, A21, A32.
Решение: 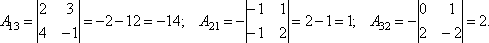
Определение. Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A-1 и удовлетворяющая условию 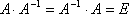 . (Это определение вводится по аналогии с умножением чисел). Понятие обратной матрицы вводится только для квадратных матриц.
. (Это определение вводится по аналогии с умножением чисел). Понятие обратной матрицы вводится только для квадратных матриц.
Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.
Итак, чтобы найти обратную матрицу нужно:
1. Найти определитель матрицы A.
2. Найти матрицу, транспонированную полученной матрице.
3. Найти алгебраические дополнения Aij всех элементов матрицы AТ и составить матрицу, элементами которой являются числа Aij.
4. Умножить матрицу, полученную в пункте 3 на 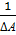
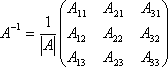
Пример 6: Найти обратную матрицу А-1, если 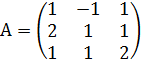 и выполнить проверку.
и выполнить проверку.
Решение: 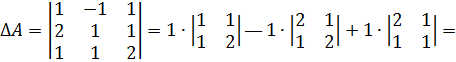
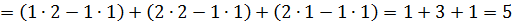
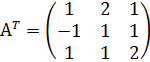 ,
, 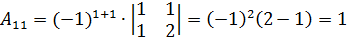 , аналогично
, аналогично 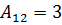 ,
, 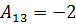 ,
, 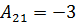 ,
, 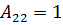 ,
, 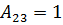 ,
, 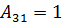 ,
, 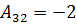 ,
, 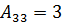
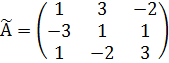 ,
, 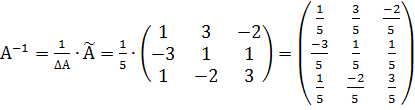 . Для проверки используется формула:
. Для проверки используется формула: 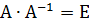 , где
, где 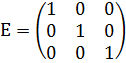 .
.
 2015-04-06
2015-04-06 23536
23536