Теорема: Если f(x) и g(x) дифферен. в точке х, то: 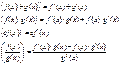
Теорема о произв. сложной функции.
Если y(x)=f(u(x)) и существует f’(u) и u’(x), то существует y’(x)=f(u(x))u’(x).
Теорема о произв. обратной функции.
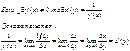
Таблица производных:
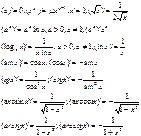
Дифференциал функции.
Определение: Если Х независимая переменная, то дифференциал функции f(x) наз. f’(x)Dx=u обозначают df(x).
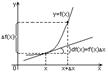
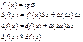
Теорема об инвариантной форме первого дифференциала.
df(x)=f’(x)dx
Доказательство:
1).
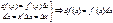
2). 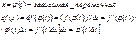
 2015-07-14
2015-07-14 258
258








