Гиперболой называется линия, имеющая в некоторой системе координат уравнение 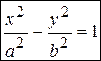 , где
, где 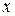 и
и 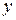 - переменные,
- переменные, 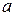 и
и 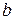 - положительные числа. Уравнение называется каноническим уравнением гиперболы.
- положительные числа. Уравнение называется каноническим уравнением гиперболы.
Отрезок 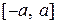 и его длина называются действительнойосью гиперболы, а отрезок
и его длина называются действительнойосью гиперболы, а отрезок 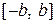 и его длина
и его длина 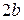 - мнимой осью.
- мнимой осью.
Гипербола симметрична относительно оси абсцисс и оси ординат.
Точки 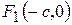 и
и 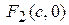 называются фокусами эллипса, причем
называются фокусами эллипса, причем 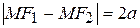 - модуль разности расстояний от фокусов до любой точки на гиперболе есть величина постоянная и равная
- модуль разности расстояний от фокусов до любой точки на гиперболе есть величина постоянная и равная 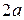 . Между
. Между 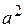 ,
, 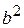 и
и 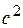 существует связь:
существует связь: 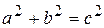 .
.
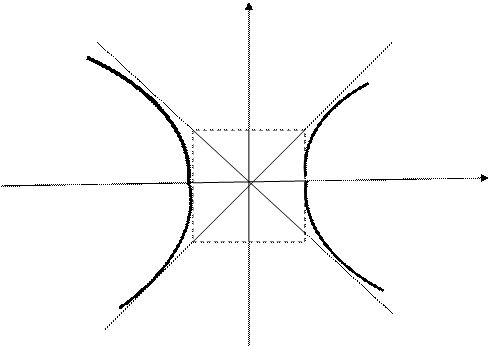
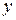
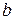
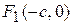
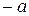
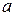
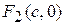
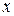
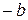
Прямые линии 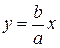 и
и 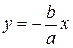 называются асимптотами гиперболы: т.е. при неограниченном увеличении
называются асимптотами гиперболы: т.е. при неограниченном увеличении 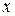 точка на гиперболе приближается к этим прямым сколь угодно близко.
точка на гиперболе приближается к этим прямым сколь угодно близко.
Уравнение гиперболы с центром в точке 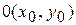 :
:
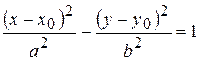 .
.
В школьном курсе математики изучались гиперболы вида 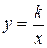 . Положение гиперболы зависит от
. Положение гиперболы зависит от 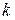 .
.
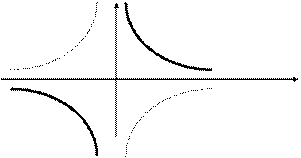 |
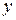
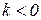
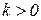
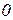
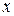
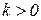
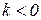
Асимптотами данной гиперболы являются прямые, проходящие через центр гиперболы: 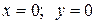 . Уравнение гиперболы с центром в точке с координатами
. Уравнение гиперболы с центром в точке с координатами 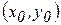 имеет вид
имеет вид 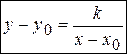 .
.
 2015-07-14
2015-07-14 322
322








