Параболой называется линия, имеющая в некоторой системе координат уравнение 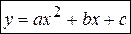 , где
, где 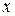 и
и 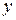 - переменные,
- переменные, 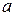 ,
, 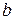 ,
, 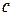 - действительные числа,
- действительные числа, 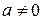 .
.
Выделив полный квадрат, получим уравнение параболы в виде 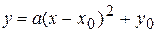 , где
, где 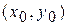 - координаты вершины параболы.
- координаты вершины параболы.
Здесь  ;
; 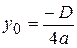 , где
, где 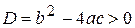 - дискриминант квадратного уравнения
- дискриминант квадратного уравнения 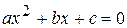 .
.
При 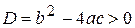 парабола пересекает ось абсцисс в двух точках, эти числа являются корнями
парабола пересекает ось абсцисс в двух точках, эти числа являются корнями 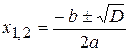 уравнения
уравнения 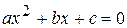 .
.
При 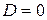 уравнение имеет один корень
уравнение имеет один корень 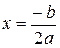 ; в этой точке парабола касается оси абсцисс
; в этой точке парабола касается оси абсцисс
При 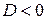 парабола не имеет с осью абсцисс общих точек.
парабола не имеет с осью абсцисс общих точек.
Парабола симметрична относительно прямой 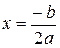 .
.
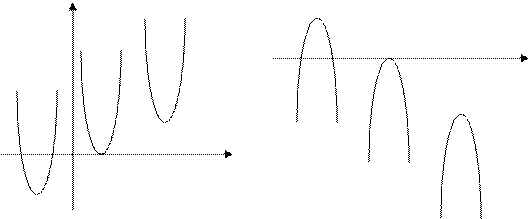
 На рисунке изображены параболы, у которых
На рисунке изображены параболы, у которых 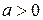 или
или 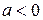 и различные значения дискриминанта.
и различные значения дискриминанта.
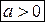
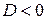
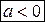
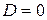
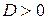
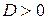
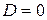
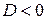
Контрольные вопросы
1. Каков признак уравнения окружности?
2. Напишите уравнения окружностей радиусом 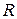 с центром в точке: а)
с центром в точке: а) 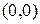 ; б)
; б)  , постройте их.
, постройте их.
3. Каков признак уравнения эллипса?
4. Напишите уравнения и постройте эллипсы с полуосями 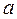 и
и 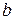 , имеющие центры: а) в точке
, имеющие центры: а) в точке 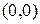 ; б) в точке
; б) в точке  .
.
5. Постройте гиперболы по уравнениям: 1) 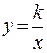 ; 2)
; 2) 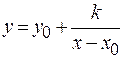 .
.
6. Запишите уравнения асимптот гипербол 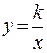 и
и  .
.
7. Каков признак уравнения параболы?
8. Постройте параболу по уравнению 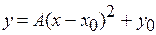 . Как влияют на положение параболы числа
. Как влияют на положение параболы числа  ?
?
9. Запишите уравнение оси симметрии параболы 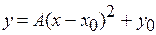 .
.
 2015-07-14
2015-07-14 746
746







