| № пункта | Координаты исходных пунктов | Измеренные углы sa = 1,0² | Измеренные расстояния sS = 0,1 м | |
| Х1, м | Х2, м | |||
| 84 396,80 | 77 632,31 | 115 55 46,1 | 18 257,32 | |
| 89 688,00 | 100 428,20 | 205 39 21,5 | 14 725,80 | |
| 66 275,02 | 93 752,04 | 1 41 40,2 | 10 143,26 |
Результаты вычислений для целевой функции (3.3) приведены в табл. 4.2, где х1, х2 ¾ уравненные координаты, V ¾ поправки в измерения.
Таблица 4.2
Результаты оценки точки прямой и линейной засечек при n = 2
| Обозначения | Прямая засечка | Линейная засечка |
| Х1 | 76 413,318 м | 76 414,018 м |
| Х2 | 94 052,006 м | 94 051,045 м |
| V1 | 0,54² | 0,073² |
| V2 | 0,99 | 0,165 |
| V3 | 0,74 | 0,181 |
| m | 1,35 | 0,255 |
| DF | 1,82 | 0,065 |
| a | 0,115 м | 0,255 м |
| b | 0,055 | 0,180 |
| Q | 4° 48¢ | 91° 30¢ |
| Q11 | 0,00725 | 0,499 |
| Q22 | 0,00171 | 1,003 |
| Q12 | 0,00047 | - 0,0132 |
| M | 0,128 м | 0,312 м |
Преимущество предложенной методики вычисления элементов эллипса ошибок заключается в том, что она пригодна не только при обработке по методу наименьших квадратов, где используется целевая функция (3.3), но и для других критериев уравнивания в соответствии с критериальной функцией (3.1) при любом n. Здесь так же применяется целевая функция (4.4), но выбирается конкретное значение, DF, которое при n = 2 равно m2. Если n ¹ 2, то теорем, в соответствии, с которыми выбирается DF, нет. В этих условиях предлагаем получать неизвестное приращение DF, считая при любом n значение большой полуоси эллипса таким же, как для случая n = 2. Следовательно, методика при n ¹ 2 будет состоять из следующих этапов: находим полуось a при n = 2; затем при n ¹ 2 определяем угол Q, не зависящий от DF; по направлению Q вычислим значение целевой функции (3.1) на расстоянии от ее минимума, равном a, и вычислим искомое DF. Так, при любом n большая полуось эллипса будет одинаковой, и следовательно, вероятность попадания в него будет близка к 0,39 ¾ вероятности попадания в средний квадратический эллипс ошибок. Результаты такой оценки точности при различных n даны в табл. 4.3 и 4.4.
Таблица 4.3.
Результаты оценки точности прямой засечки при n ¹ 2
| Обозначения | n = 1 | n = 3 | n = 4 |
| Х1 | 76 413,389 м | 76 413,306 м | 76 413,301 м |
| Х2 | 94 051,971 м | 94 052,007 м | 94 052,007 м |
| V1 | 0² | 0,66² | 0,71² |
| V2 | 1,85 | 0,89 | 0,86 |
| V3 | 0,78 | 0,79 | |
| m | 1,85 | 1,36 | 1,37 |
| DF | 0,523 | 2,46 | 3,35 |
| A | 0,115 м | 0,115 м | 0,115 м |
| B | 0,026 | 0,038 | 0,033 |
| Q | 115° 56¢ | 9° 08¢ | 10° 04¢ |
| Q11 | 0,00090 | 0,00699 | 0,00685 |
| Q22 | 0,00316 | 0,00094 | 0,00078 |
| Q12 | - 0,00144 | 0,00100 | 0,00111 |
| M | 0,118 м | 0,121 м | 0,120 м |
Таблица 4.4.
Результаты оценки точности линейной засечки при n ¹ 2
| Обозначения | n = 1 | n = 3 | n = 4 |
| Х1 | 76 414,185 м | 76 414,006 м | 76 414,001 м |
| Х2 | 94 052,045 м | 94 052,078 м | 94 052,091 м |
| V1 | 0² | 0,108² | 0,122² |
| V2 | 0,013 | 0,162 | 0,160 |
| V3 | 0,348 | 0,169 | 0,165 |
| m | 0,348 | 0,258 | 0,260 |
| DF | 0,0441 | 0,0338 | 0,0130 |
| A | 0,255 м | 0,255 м | 0,255 м |
| B | 0,0314 | 0,191 | 0,201 |
| Q | 17° 39¢ | 89° 51¢ | 83° 04¢ |
| Q11 | 0,488 | 0,548 | 0,603 |
| Q22 | 0,0567 | 0,477 | 0,957 |
| Q12 | 0,153 | 0,00112 | 0,0436 |
| M | 0,257 м | 0,319 м | 0,324 м |
Данная методика устойчива при любом качестве засечек и не дает деления на ноль даже в вырожденном случае. Подтвердим сказанное на примере обратной засечки на плоскости, у которой все пункты лежат на одной окружности (рис. 4.2)
|
Рис. 4.2. Обратная засечка
Допустим, что методом нелинейного программирования получен минимум целевой функции в точке М. По изолинии, выделенной на рис. 4.2 между исходными пунктами 1 и 4, будет найден эллипс, по размерам которого убедимся в плохом качестве засечки, и деления на ноль не произойдет. Следовательно, методы нелинейного программирования не требуют применения регуляризации для вырожденных случаев.
 2015-07-14
2015-07-14 664
664

 2 3
2 3


 1 4
1 4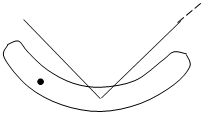
 M
M






