Соединительные точки между сегментами бывают нескольких типов. В одном случае требуется обеспечить соединение криволинейного сегмента с прямым, в другом - получить идеально гладкое сочленение (сопряжение) без стыка или перегиба. В качестве образцов опорных точек составим таблицу для следующих векторных программ, использующих кривые Безье: CorelDRAW, Adobe Illustrator и Macromedia FreeHand. Типы опорных точек в трехмерной графике представлены на примере Autodesk 3D МАХ.
Тип опорной точки, соединяющий два сегмента и обеспечивающий независимость управляющих точек по направлению и длине друг от друга, называется изгибом (рис. 14).
В программе CorelDRAW такая точка называется перегиб (cusp). В других программах: угловая (corner).
Угловое сочленение сегментов (изгиб) не всегда разумно и выгодно. Например, для создания окружности необходимо обеспечить соединение, которое называют гладким сопряжением, когда одна кривая плавно переходит в другую. Такое сочление обеспечивает гладкая опорная точка (smooth) (рис. 15). Условием этого являются управляющие линии, лежащие на одной прямой. У такой точки направление управляющих линий фиксировано относительно друг друга, при перемещении одной управляющей линии другая также движется синхронно как рычаг. Вместе с тем, такие управляющие линии могут различаться по величине.
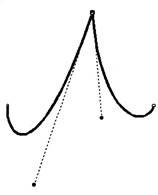

| Рис. 14.Пример точки перегиба | Рис. 15.Пример гладкой точки |
У программы CorelDRAW предусмотрен подвид гладкого сочленения, который называется симметричный узел (symm от слова "symmetrical") (рис. 16). Суть его состоит в том, что управляющие линии фиксируют не только по направлению, но и по величине (длина направляющих всегда одинакова). Если одну из них увеличивать или уменьшать, другая будет синхронно повторять это действие. В программах Adobe Illustrator и Macromedia Freehand такой тип опорной точки отсутствует, хотя его можно получить вручную.
В свою очередь, у программы FreeHand в отдельный вид опорных точек выделен случай гладкого сочленения прямолинейного и криволинейного сегментов (рис. 17). Такая точка получила название тангенциальной (connecter point). При выделении такая точка обозначается треугольником. Для того чтобы криволинейный сегмент гладко сопрягался с прямой линией, касательная криволинейного сегмента должна совпасть с продолжением прямого сегмента. Поэтому управляющая точка криволинейного сегмента способна двигаться только вдоль этой касательной. В программах CorelDRAW и Adobe Illustrator такое соединение также имеет место, но не выделено в специальный тип опорной точки.
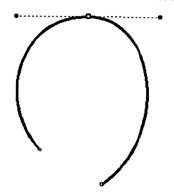
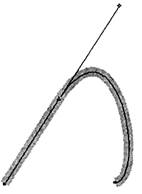
| Рис. 16.Симметричная опорная точка | Рис. 17.Пример тангенциальной точки в программе FreeHand |
Типы опорных точек можно суммировать в виде следующей таблицы (табл. 1).
Таблица 1. Типы опорных точек в различных векторных программах
| Тип опорной точки | Adobe Illustrator | Macromedia FreeHand | CorelDRAW |
| Угловая | Corner anchor point | Corner point | Cusp node |
| Гладкая | Smooth anchor point | Curve point | Smooth node |
| Тангенциальная | — | Connector point | — |
| Симметричная | — | — | Symm node |
Типы опорных точек в трехмерной графике имеют ту же основу, но отличаются другими характеристиками (программа Autodesk 3D МАХ).
- Smooth (гладкая): вершина, через которую кривая проходит "неуправляемо" гладко. Форма кривой определяется расстоянием между соседними вершинами.
- Corner (угловая): вершина, в которой кривая получает излом.
- Bezier (Безье): вершина Безье с управляющими рычагами, которые не равны по длине, но ориентированы строго в противоположных направлениях. Форма кривой зависит и от направления касательных, и от длины рычагов.
- Bezier Corner (угловая Безье): все характеристики идентичны опорной точке Bezier, но угол между управляющими рычагами может быть произвольным, т. е. допускается излом на кривой.
Историческая справка о кривых*
В докомпьютерные времена специалисты, которые работали с линейными изображениями (архитекторы, кораблестроители и инженеры) для создания своих проектов пользовались только бумагой, карандашами и простейшими чертежными инструментами (линейками, циркулями, угольниками и транспортирами). Однако при создании чертежей больших деталей в натуральную величину, например шпангоутов судов, возникали естественные сложности. Причем проблема состояла не только в размере, но скорее в том, чтобы провести гладкую кривую через определенное количество заранее фиксированных точек.
Решение было найдено: в больших помещениях нужную форму кривой получали, выгибая длинные тонкие полоски дерева или металла. Такие полоски называли сплайнами (splines). Для того чтобы придать упругой полоске нужную форму, ее фиксировали в требуемых точках с помощью особых свинцовых грузил, которые за сходство формы назывались " утятами " (ducks). Результирующая кривая получалась гладкой, а форма изменялась перемещением грузил (рис. 18).
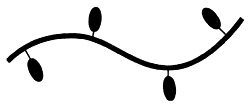
Рис. 18. Чертежные сплайны
Впоследствии понятие сплайна стали применять в математике для похожей цели — описания кривых.
В 1885 году Карл Вейерштрасс[2] сформулировал и доказал теорему, названную его именем. Примерно в таком виде она приводится в современных курсах математического анализа: в соответствии с этой теоремой для любой непрерывной на отрезке функции найдется многочлен, сколь угодно мало отличающийся от данной функции. В более простой формулировке это означает, что согласно доказанной теореме Вейерштрасса можно обрисовать любую функцию с помощью полиномов[3].
Вопрос о построении аппроксимирующего многочлена привлек многих математиков. Среди них одну из решающих ролей сыграл выдающийся ученый Сергей Натанович Бернштейн[4], который в начале XX века предложил новое доказательство теоремы Вейерштрасса с помощью теории вероятностей. В этом случае необходимый полином строится в явном виде (не параметрически). Именно данный полином и стал основой сплайновых кривых, в частности NURBS-кривых и кривых Безье.
Теперь все компьютерные художники и дизайнеры знают "кривые Безье", "инструменты Безье".
Резюме
Ø Кривые Безье получили широкое распространение, т. к. обладают следующими важными свойствами:
o начальная и конечная контрольные точки лежат на кривой;
o кривая на всем протяжении непрерывна, у нее отсутствуют разрывы;
o касательные к кривой в начальной и конечной контрольных точках являются отрезками, соединяющими их с двумя другими соседними контрольными точками;
o кривая всегда располагается внутри выпуклого многоугольника из ее контрольных точек
Ø Для построения кривой Безье требуются четыре контрольных точки, хотя кривая физически проходит только через две из них (опорные точки). Две точки остаются в стороне (управляющие точки).
Ø Кривая Безье - это вектор. Поэтому она располагает начальной и конечной точками. Направление контуров находит свою реализацию в составных контурах (compound paths).
Ø Соединительные точки между сегментами бывают нескольких типов, что позволяет обеспечить различные формы соединения (гладкую, тангенциальную или на изгиб).
Вопросы для конспектирования:
1. Сколько контрольных точек и какие требуются для построения кривой Безье?
2. Для чего программе нужно знать положительную или отрицательную сторону линии, поверхности?
3. Дайте сравнительную характеристику кривых Безье и NURBS-кривых. Подчеркните достоинства и недостатки.
4. Охарактеризуйте принцип линейной аппроксимации.
5. Перечислите все типы опорных точек, используемых различными векторными программами.
1. Составьте развернутый конспект лекции.
2. Дополните таблицу 1 сведениями из других программ векторной графики.
*** Задание выполните в рабочей тетради.
[1] См. лекцию № 2 «Принципы векторной графики»
[2] Вейершрасс Карл (1815—1897) — немецкий математик, иностранный член-корреспондент (1864) и иностранный почетный член (1895) Петербургской Академии Наук. Известен своими трудами в области математического анализа, теории функций и линейной алгебры. Главным его научным достижением считается система логического обоснования математического анализа.
[3] Слово полином - от греческого слова poly (многочисленный) и латинского слова nomen (имя); русский эквивалент этого понятия - многочлен. Полином представляет собой алгебраическую сумму конечного числа одночленов, например, для одной переменной х многочлен имеет вид: y = a0xn +a1xn-1...+an, где а — коэффициенты многочлена, п — показатель степеней (целые неотрицательные числа).
[4] Бернштейн Сергей Натанович (1880—1968)— математик, академик Академии Наук СССР и Академии Наук Украины. Основные труды относятся к области теории дифференциальных уравнений (условия аналитичности решений), теории функций (приближение функций многочленами), теории вероятностей (аксиоматика, предельные теоремы).
 2015-07-14
2015-07-14 4581
4581