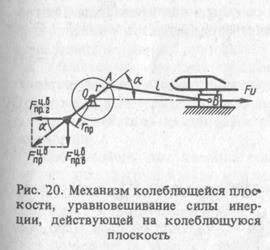
На рис. 20 показан кривошипно-шатунный механизм с ползуном, используемый и для привода колеблющейся плоскости. Известна формула для расчета ускорения ползуна
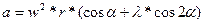 . (V-24)
. (V-24)
где 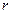 — радиус кривошипа;
— радиус кривошипа; 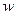 - угловая скорость кривошипа;
- угловая скорость кривошипа; 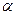 - угол поворота кривошипа от начального положения (см, рис. 20).
- угол поворота кривошипа от начального положения (см, рис. 20).
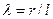 ,
,
где 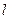 - длина шатуна.
- длина шатуна.
Сила инерции, действующая на колеблющуюся плоскость, массой 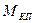 равна
равна 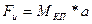 или
или
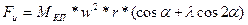 . (V-25)
. (V-25)
Эту силу инерции можно представить в виде двух сил:
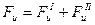 (V-26)
(V-26)
Сила 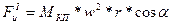 называется силой инерции первого порядка, сила
называется силой инерции первого порядка, сила 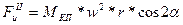 - силой инерции второго порядка, так как частота ее изменения вдвое превосходит частоту изменения силы инерции первого порядка. Максимальное значение силы инерции второго порядка составляет не более чем
- силой инерции второго порядка, так как частота ее изменения вдвое превосходит частоту изменения силы инерции первого порядка. Максимальное значение силы инерции второго порядка составляет не более чем 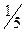 максимального значения силы инерции первого порядка, потому что
максимального значения силы инерции первого порядка, потому что 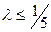 .
.
Силы инерции, приложенные к ползуну, т. е. к колеблющейся плоскости, передаются через кинематические пары, шатун, кривошип на станину машины, далее на фундамент и здание. Чтобы уменьшить действие инерционных сил на станину машины, а также на фундамент и здание, уравновешивают инерционные силы.
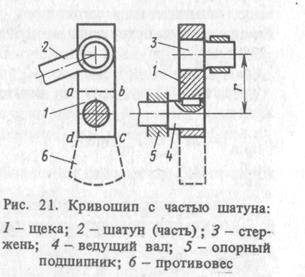
Начнем с уравновешивания вращающихся масс. На рис. 21 дан кривошип с частью шатуна. Массы в контуре 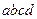 уравновешены относительно оси вала. Массы за пределами контура не уравновешены: это массы верхней части щеки, стержня, части шатуна. Неуравновешенные массы кривошипа приводят к одной массе, лежащей на расстоянии
уравновешены относительно оси вала. Массы за пределами контура не уравновешены: это массы верхней части щеки, стержня, части шатуна. Неуравновешенные массы кривошипа приводят к одной массе, лежащей на расстоянии 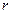 от оси вращения кривошипа; для приведения используют формулу
от оси вращения кривошипа; для приведения используют формулу
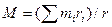 (V-27)
(V-27)
Для вычисления всех вращающихся, но неуравновешенных масс следует учесть и массу шатуна. Так как шатуны пищевых машин имеют форму параллелепипеда, то массу шатуна М следует разделить на две равные части: при расчетах одна присоединяется к ползуну, другая — к кривошипу.
Итак, масса неуравновешенных вращающихся частей
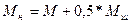 . (V-28)
. (V-28)
На массу 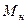 при вращении действует центробежная сила
при вращении действует центробежная сила
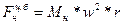 , (V-29)
, (V-29)
направление которой зависит от положения кривошипа. Эта сила не уравновешена и буквально "дергает во все стороны" опорный подшипник. Чтобы уравновесить эту силу, необходимо на продолжении кривошипа закрепить противовес массой 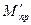 . Если центр массы противовеса находится на расстоянии
. Если центр массы противовеса находится на расстоянии 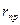 от оси вращения кривошипа, то на противовес будет действовать сила
от оси вращения кривошипа, то на противовес будет действовать сила
 (V-30)
(V-30)
Чтобы на ось кривошипа (точку 0) не действовала сила, надо, чтобы 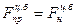 , тогда
, тогда
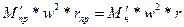 (V-31)
(V-31)
откуда
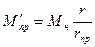 (V-32)
(V-32)
Размещение противовеса показано на рис. 21 пунктиром (деталь 6).
Итак, определив 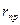 и
и 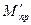 , уравновешиваем вращающиеся части кривошипа.
, уравновешиваем вращающиеся части кривошипа.
Перейдем к уравновешиванию сил инерции, возникающих от возвратно-поступательного движения ползуна — колеблющейся плоскости. На рис. 20 показан кривошипно-шатунный механизм с инерционной силой 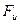 , действующей на ползун. Сила инерции
, действующей на ползун. Сила инерции 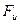 может быть разложена на силы инерции первого и второго порядков. Сила инерции первого порядка, у которой частота изменения равна частоте вращения ведущего вала, вычисляется по формуле
может быть разложена на силы инерции первого и второго порядков. Сила инерции первого порядка, у которой частота изменения равна частоте вращения ведущего вала, вычисляется по формуле
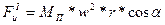 (V-33)
(V-33)
где 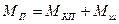 .
.
Эта сила, передаваясь через стержни и кинематические пары, действует на опорный подшипник. Для ее уравновешивания надо применить второй противовес, масса которого, например, равна 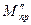 , и ее центр масс находится на расстоянии
, и ее центр масс находится на расстоянии 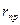 от оси вращения кривошипа. Центробежная сила, действующая на противовес, будет равна
от оси вращения кривошипа. Центробежная сила, действующая на противовес, будет равна
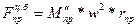 (V-34)
(V-34)
Разложим эту силу на вертикальную и горизонтальную составляющие:
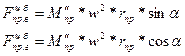 (V-35)
(V-35)
Конструктор всегда может так подобрать массу 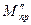 и расстояние
и расстояние 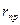 , что удастся получить равенство
, что удастся получить равенство 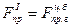 , тогда
, тогда
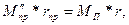 (V-36)
(V-36)
отсюда
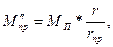 (V-37)
(V-37)
Учитывая равенство (V - 36), необходимо сделать вывод, что в горизонтальном направлении силы на станину (опорный подшипник) не действуют.
Однако существует вертикальная составляющая центробежной силы (V - 35), которую ничто не уравновешивает, и при угле поворота кривошипа 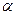 = 90° она получает максимальное значение
= 90° она получает максимальное значение
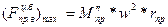 (V-38)
(V-38)
равное максимальному значению силы инерции ползуна первого порядка. Таким образом, полное уравновешивание силы инерции ползуна первого порядка приводит к появлению новой вертикальной силы, которая действует на станину с той же силой, что и неуравновешенная сила инерции ползуна.
Поэтому при уравновешивании однокривошипного механизма применяют частичное уравновешивание. Массу противовеса, например, определяют из следующего равенства [сопоставить с равенством (V - 36)]:
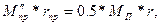 (V-39)
(V-39)
В этом случае вредное воздействие сил инерции на станину машины уменьшается в 2 раза, правда, при этом появляется вертикальная периодическая сила, равная половине силы инерции первого порядка.
Таким образом, уравновешивая вращающиеся массы, определили массу противовеса 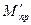 [формула (V - 32)], а также, уравновешивая массы ползуна, вычислили
[формула (V - 32)], а также, уравновешивая массы ползуна, вычислили 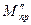 . При конструировании механизма обе массы объединяют в одной детали-противовесе, и его масса
. При конструировании механизма обе массы объединяют в одной детали-противовесе, и его масса
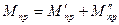 (V - 40)
(V - 40)
Из вышеизложенного следует, что полного уравновешивания одно-кривошипного механизма достичь невозможно. Поэтому применяют двух-кривошипную схему с оппозитно движущимися ползунами (рис. 22), так называемый самоуравновешенный механизм. Схема показывает, что от одного вала приводятся в движение два механизма ОАВ и OCD. При равных размерах и массах звеньев силы инерции 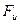 равны, и результат их воздействия на опорный подшипник, помещенный в точке О, равен нулю.
равны, и результат их воздействия на опорный подшипник, помещенный в точке О, равен нулю.
Компенсация сил инерции колеблющейся плоскости пружинами служит для разгрузки всех кинематических пар, шатуна и кривошипа от вредного воздействия сил инерции ползуна. Сила инерции ползуна вынуждает конструктора увеличить сечения звеньев механизма. Из-за этой силы инерции появляются повышенные давления в подшипниках, расположенных в местах кинематических пар. В результате увеличивается трение и повышается расход энергии.
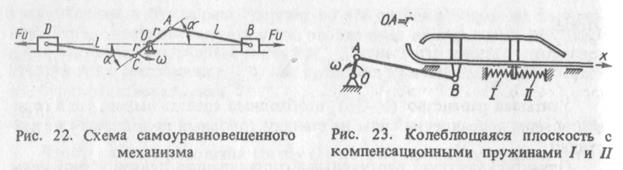
Для того чтобы разгрузить детали от вредного действия силы 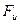 , устанавливают компенсационные пружины. При малых значениях инерционной силы вместо пружин можно поставить резиновые жгуты. Схема установки компенсационных пружин показана на рис. 23.
, устанавливают компенсационные пружины. При малых значениях инерционной силы вместо пружин можно поставить резиновые жгуты. Схема установки компенсационных пружин показана на рис. 23.
Жесткость одной компенсационной пружины
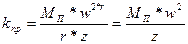 (V - 41)
(V - 41)
где 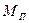 - масса колеблющейся плоскости, z - число компенсационных пружин; оно всегда четное.
- масса колеблющейся плоскости, z - число компенсационных пружин; оно всегда четное.
Часто для компенсации сил инерции колеблющейся плоскости используют рессоры. Рессорой называется пластина, предназначенная для подвешивания узла машины, в частности колеблющейся, плоскости. Один конец рессоры консольно закрепляется на станине, другой - шарнирно связывается с колеблющейся плоскостью.
Если разъединить шарнир В, плоскость с пружинами станет свободной. На рис. 23 плоскость изображена в нейтральном положении. Если вывести плоскость из нейтрального положения, т. е. сместить ее на расстояние x и освободить, она под действием пружин перейдет в движение и станет колебаться. Определим частоту собственных колебаний плоскости.
Для решения этой задачи составим дифференциальное уравнение и примем начальные условия, которые удобно привязать к нейтральному положению; тогда при 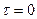 смещение плоскости х = 0, а ее скорость будет максимальной
смещение плоскости х = 0, а ее скорость будет максимальной 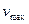 . Величина максимальной скорости при движении плоскости в составе механизма не может быть выше
. Величина максимальной скорости при движении плоскости в составе механизма не может быть выше 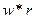 , значит, при
, значит, при 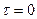
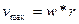 .
.
Составим дифференциальное уравнение движения плоскости на основании второго закона механики:
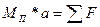 ,
,
где 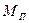 - масса плоскости;
- масса плоскости; 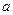 — ускорение плоскости;
— ускорение плоскости; 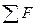 - сумма всех сил, приложенных к плоскости.
- сумма всех сил, приложенных к плоскости.
На плоскость при движении действуют силы упругости пружин 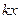 , силы трения, пропорциональные скорости движения
, силы трения, пропорциональные скорости движения 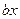 . Поэтому
. Поэтому
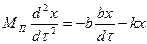 (V - 42)
(V - 42)
Это уравнение второго порядка. В условиях нашей задачи можно пренебречь сопротивлениями, тогда уравнение примет вид
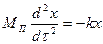 (V - 43)
(V - 43)
Все члены уравнения надо перенести в левую сторону а коэффициент при первом члене привести к единице, тогда
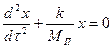 . (V - 44)
. (V - 44)
Чтобы решить дифференциальное уравнение, составим характеристическое уравнение
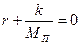 (V - 45)
(V - 45)
Для удобства решения характеристического уравнения обозначим
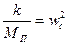 (V - 46)
(V - 46)
Тогда 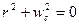 и корни уравнения (V - 45) будут равны
и корни уравнения (V - 45) будут равны
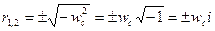 (V – 47)
(V – 47)
или
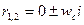 (V – 48)
(V – 48)
Значит, общее решение уравнения (V - 44) будет таким:
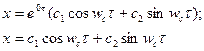 (V – 49)
(V – 49)
где 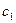 и
и 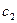 - постоянные интегрирования, которые надо определять по начальным условиям.
- постоянные интегрирования, которые надо определять по начальным условиям.
Мы уже знаем, что при 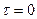
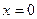 ; подстановка этих значений в (V -49) дает
; подстановка этих значений в (V -49) дает 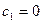 .
.
Далее при 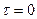
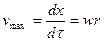 . Дифференцируем общее решение (V - 49) и получаем
. Дифференцируем общее решение (V - 49) и получаем
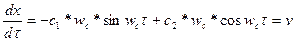
Подставив начальные условия, получим
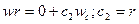 .
.
Найденные значения постоянных интегрирования 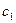 и
и 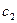 подставляем в уравнение (V - 45) и получаем частное (окончательное) решение дифференциального уравнения движения свободной колеблющейся плоскости:
подставляем в уравнение (V - 45) и получаем частное (окончательное) решение дифференциального уравнения движения свободной колеблющейся плоскости:
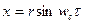 . (V - 50)
. (V - 50)
Видно, что колебания гармонические. Если 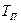 (в с) - период колебаний, то через
(в с) - период колебаний, то через 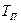 плоскость возвратится в то же самое положение. Следовательно,
плоскость возвратится в то же самое положение. Следовательно,
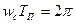
отсюда 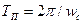 и с учетом (V - 46) получаем
и с учетом (V - 46) получаем
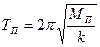 (V - 51)
(V - 51)
Частоту - величину, обратную периоду, для собственных колебаний плоскости - вычисляют по формуле
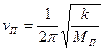 (V - 52)
(V - 52)
Таким образом, частота собственных колебаний колеблющейся плоскости возрастает с увеличением жесткости пружины и с уменьшением массы колеблющейся плоскости. Если частота собственных колебаний плоскости равна частоте вращения кривошипа 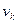 , от которого приводится колеблющаяся плоскость, наступает резонанс. Чтобы избежать резонанса, необходимо изменить частоту собственных колебаний плоскости. Для этого следует изменить жесткость пружин или массу плоскости. Необходимо,чтобы
, от которого приводится колеблющаяся плоскость, наступает резонанс. Чтобы избежать резонанса, необходимо изменить частоту собственных колебаний плоскости. Для этого следует изменить жесткость пружин или массу плоскости. Необходимо,чтобы 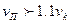 или
или 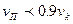 .
.
 2015-07-14
2015-07-14 1429
1429








