При использовании кинетического подхода к моделированию динамической характеристики воспользуемся характеристикой пропорционального звена (53) дополнив ее членом, учитывающим запаздывание реагирования (скорость изменения выходного сигнала).
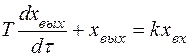 , (54)
, (54)
где Т – временной параметр, 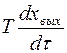 – учитывает временную задержку показаний.
– учитывает временную задержку показаний.
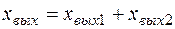 (55)
(55)
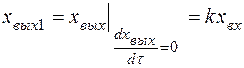 (56)
(56)

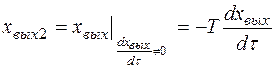 (57)
(57)
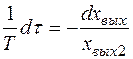
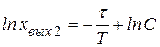
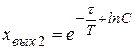 (58)
(58)
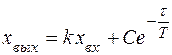 (59)
(59)
 При
При 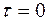 ,
, 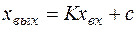 , если
, если 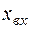 =0,то
=0,то 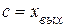
Подставляем полученное выражение в формулу (59)
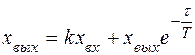 (60)
(60)
Выразим 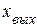 :
:
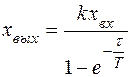 (61)
(61)
Так как при 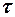 =0,
=0, 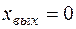 , то
, то 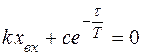
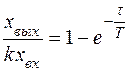 (62)
(62)
Если измеряемая величина изменяется в пределах 0,95 от установившегося значения, то измерения можно считать статическими.
При 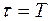 :
:
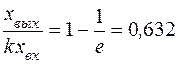 (63)
(63)
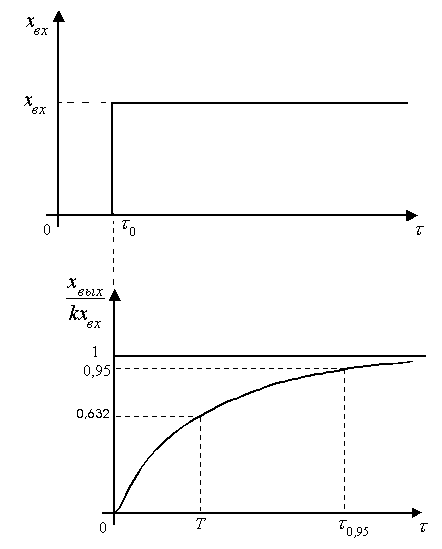
T – время, по истечении которого выходное значение сигнала достигнет 0,632 от установившегося. Т называют постоянной времени. Ее обычно заносят в паспорт прибора (динамический показатель). Иногда указывают частоту сигнала, при которой погрешность не превысит 5%.
На нижеследующем рисунке представлен график функции (62).
|
| Рисунок 8 |
Примеры апериодических звеньев:
- преобразователи температуры (термометры);
- электрохимические элементы (звенья) измерительных систем.
2.2 Периодические звенья
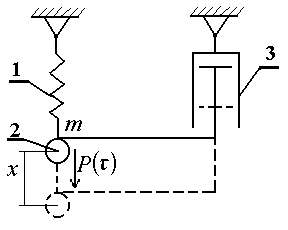
Пример: Система пружинных весов
|
Рисунок 9 – Система пружинных весов:
1 – пружина, 2 – масса всех элементов 3 – демпфер, 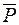 – действующая сила, после приложения которой весы меняют свое положение – действующая сила, после приложения которой весы меняют свое положение 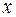 – перемещение (текущая координата), – перемещение (текущая координата), 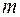 – приведенная масса элементов системы, – приведенная масса элементов системы, 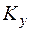 – коэффициент трения – коэффициент трения
|
Для анализа воспользуемся уравнениями статики:
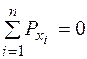 , (64)
, (64)
где 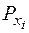 – проекции сил
– проекции сил
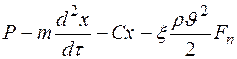
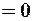 (65)
(65)
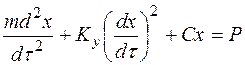 (66)
(66)
Отметим, что 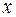 – отклонение колеблющейся точки от положения равновесия. Известно, что линейная комбинация частных решений дифференциального уравнения есть также решение данного уравнения. Общее решение дифференциальных уравнений второго порядка есть итог двух интегрирований. Стало быть полное решение уравнения второго порядка можно представить как линейную комбинацию двух частных решений:
– отклонение колеблющейся точки от положения равновесия. Известно, что линейная комбинация частных решений дифференциального уравнения есть также решение данного уравнения. Общее решение дифференциальных уравнений второго порядка есть итог двух интегрирований. Стало быть полное решение уравнения второго порядка можно представить как линейную комбинацию двух частных решений:
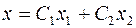 , (67)
, (67)
где 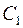 и
и 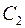 – произвольные постоянные.
– произвольные постоянные.
При этом 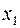 и
и 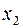 должны быть независимыми. Для нахождения независимых решений используют методику Эйлера, основывающуюся на свойстве пропорциональности экспоненты своим производным. В соответствии с указанной методикой частные решения ищут в виде
должны быть независимыми. Для нахождения независимых решений используют методику Эйлера, основывающуюся на свойстве пропорциональности экспоненты своим производным. В соответствии с указанной методикой частные решения ищут в виде
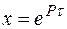 (68)
(68)
Поиск решения в этом варианте сводится к определению постоянной P. После подстановки 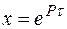 в уравнение свободных колебаний и сокращения на величину e получим квадратное уравнение
в уравнение свободных колебаний и сокращения на величину e получим квадратное уравнение
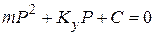 (69)
(69)
Решение уравнения – искомая константа P. Из алгебры известно, что при решении квадратного уравнения могут иметь место различные случаи в зависимости от знака дискриминанта.
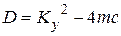 (70)
(70)
Если 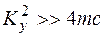 , т.е. трение велико, уравнение имеет вещественные корни
, т.е. трение велико, уравнение имеет вещественные корни 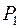 ,
, 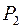 , оба корни отрицательные.
, оба корни отрицательные.
Обозначим 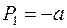 ,
, 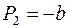 . Тогда общее решение уравнения свободных колебаний представится в виде:
. Тогда общее решение уравнения свободных колебаний представится в виде:
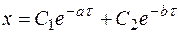 (71)
(71)
Отсюда вывод: при большом трении отклонение точки от положения равновесия с течением времени приближается к нулю по экспоненциальному закону.
С учетом правой части уравнения будем иметь:
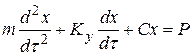 (71)
(71)
При 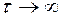
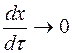
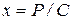 . График решения показан на рисунке 10, б.
. График решения показан на рисунке 10, б.
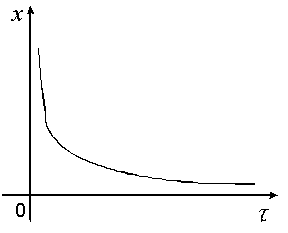 а)
а)
| 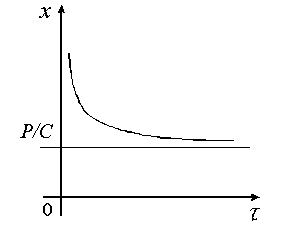 б)
б)
|
| Рисунок 10 |
Если трение мало, т.е. 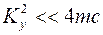 , то характеристическое уравнение имеет линейные сопряженные корни
, то характеристическое уравнение имеет линейные сопряженные корни 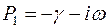 ,
, 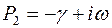 , где
, где 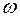 – угловая частота (в данном случае характеризует собственную частоту колебаний в системе). Общее решение:
– угловая частота (в данном случае характеризует собственную частоту колебаний в системе). Общее решение:
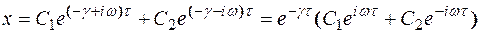 (72)
(72)
Получим 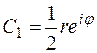 ,
, 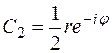 Тогда:
Тогда:
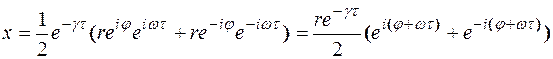 (73)
(73)
Воспользуемся формулой Эйлера и получим:
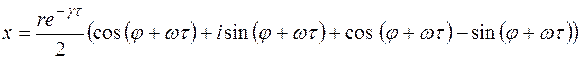 (74)
(74)
Уравнение (74) записать в ином виде:
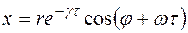 (75)
(75)
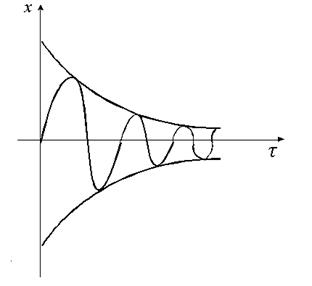
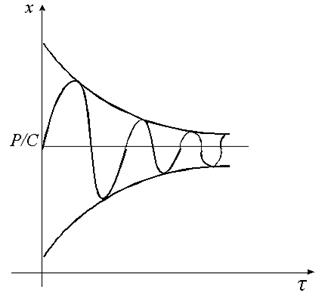
| 
|
| Рисунок 11 | Рисунок 12 |
 2015-07-14
2015-07-14 514
514








