Обобщенные силы и обобщенные перемещения

Работа постоянной силы F на перемещений 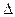по ее направлению равна произведению величины силы на указанное перемещение: .

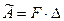В задачах механики внешняя нагрузка отличается большим разнообразием и обычно представляет собой группы сил. Выражения для какой-либо группы постоянных сил можно представить в виде произведения двух величин:

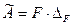, (2.1)

одна из которых – F – зависит только от сил группы и называется обобщенной силой, а другая - 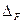- зависит от перемещений и называется обобщенным перемещением.

Таким образом, под обобщенной силой будем понимать любую нагрузку (сосредоточенные силы, сосредоточенные пары, распределенную линейную нагрузку, распределенную моментную нагрузку), а под обобщенным перемещением – тот вид перемещения, на котором обобщенная сила производит работу.

Обобщенные перемещения принято обозначать буквам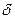и или 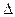с двумя индексами. Первый индекс обозначает точку и направление перемещения, а второй указывает причину, вызвавшую искомое перемещение. Например, 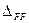обозначает перемещение точки приложения силы F по направлению ее действия, вызванное этой же силой.

Для обозначения полного перемещения точки, вызванного несколькими обобщенными силами, при 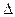сохраняется только первый индекс.

Перемещение, вызванное безразмерной единичной силой 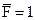или безразмерной единичной парой 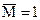, обозначается символом 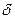и называется удельным.